Question

Vận dụng kiến thức hình học, tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh trong hai trường hợp ở C5 khi vật có chiều cao h = 6mm.

Answer 1

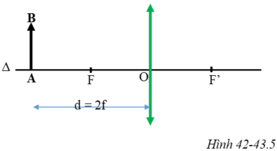
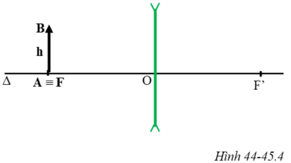
Ta đặt: OA = d; OA’ = d’; OF = OF’ = f

- Thấu kính là hội tụ.

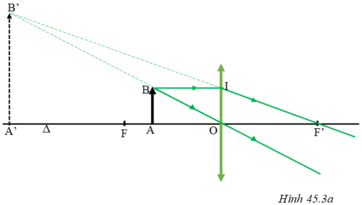
Trên hình 45.3a, xét hai cặp tam giác đồng dạng:

ΔA’B’F’ và ΔOIF’; ΔOAB và ΔOA’B’.

Từ hệ thức đồng dạng ta có:

Vì AB = OI (tứ giác BIOA là hình chữ nhật)

↔ dd' + df = d'f (2)

Chia cả hai vế của (2) cho tích d.d’.f ta được:

(đây được gọi là công thức thấu kính cho trường hợp ảnh ảo)

Thay d = 8cm, f = 12cm ta tính được: OA’ = d’ = 24cm

Thay vào (*) ta được:

+ Thấu kính là phân kỳ.

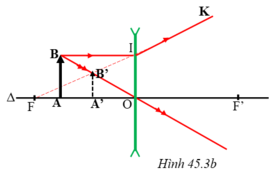
Trên hình 45.3b, xét hai cặp tam giác đồng dạng:

ΔA’B’F và ΔOIF; ΔOAB và ΔOA’B’.

Từ hệ thức đồng dạng ta có:

Vì AB = OI (tứ giác BIOA là hình chữ nhật)

↔ df' – dd' = d'f (2)

Chia cả hai vế của (2) cho tích d.d’.f ta được:

(đây được gọi là công thức thấu kính phân kỳ)

Thay d = 8cm, f = 12cm ta tính được: OA’ = d’ = 4,8cm

Thay vào (**) ta được:  = 3,6mm = 0,36cm