\(20162017.20162019=\left(20162018-1\right)\left(20162018+1\right)\)
\(=20162018^2-1< 20162018^2\)
\(\Rightarrow20162017.20162019< 20162018^2\)
Vậy...
Ta có:
\(20162017=20162018-1\)
\(20162019=20162018+1\)
\(\Rightarrow20162017.20162019\)
\(=\left(20162018-1\right).\left(20162018+1\right)\)
\(=20162018^2-1^2=20162018^2-1\)
\(\Rightarrow20162018^2-1< 20162018^2\)
Do đó \(20162017.20162018< 20162018^2\)
Chúc bạn học tốt!!!
\(\text{20162017 . 20162019}=\left(20162018-1\right)\left(20162018-1\right)\)
\(=20162018^2-1< 20162018^2\)
\(\Rightarrow20162017\cdot20162019< 20162018^2\)
Vậy .... \(20162017\cdot20162019< 20162018^2\)
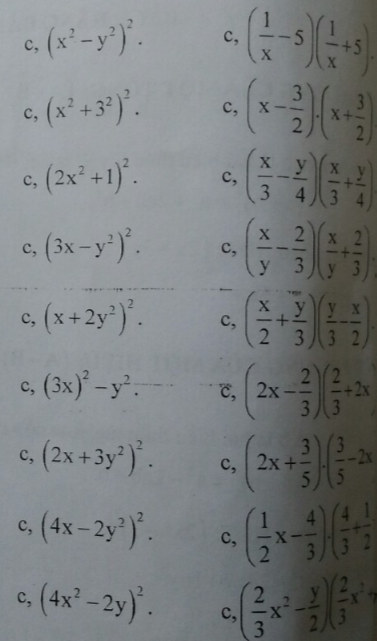viết lại các đa thức thành các vế kia hằng đẳng thức giúp em với ạ em đang cần gấp 
