a, HS tự chứng minh
b, Chi ra rằng A,H,O cùng nằm trên đường thẳng vuông góc với BC;
c, Để H ∈ (O) thì OH = OC => C O A ^ = 60 0

a, HS tự chứng minh
b, Chi ra rằng A,H,O cùng nằm trên đường thẳng vuông góc với BC;
c, Để H ∈ (O) thì OH = OC => C O A ^ = 60 0
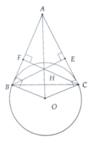
Từ một điểm A ở ngoài đường thẳng (O;R) kẻ 2 tiếp tuyến AB,AC(với B,C là các tiếp điểm). Kẻ BE vuông góc với AC, CF vuông góc với AB(E thuộc AC; F thuộc AB), BE và CF cắt nhau tại H
a, Chứng minh tứ giác BOCH là hình thoi
b, Chứng minh 3 điểm A,H,O thẳng hàng
c, Xác định vị trí điểm A để H nằm trên (O)
Từ điểm A ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến AB, AC (với B và C là các tiếp điểm). Kẻ
BE vuông AC và CF vuông AB ( E thuộc AC, F thuộc AB ), BE và CF cắt nhau tại H.
1. Chứng minh tứ giác BOCH là hình thoi.
2. Chứng minh ba điểm A, H, O thẳng hàng.
Từ điểm A ở ngoài đường tròn (O; R) kẻ hai tiếp tuyến AB, AC (với B và C là các tiếp điểm). Kẻ
BE vuông AC và CF vuông AB ( E thuộc AC, F thuộc AB ), BE và CF cắt nhau tại H.
1. Chứng minh tứ giác BOCH là hình thoi.
2. Chứng minh ba điểm A, H, O thẳng hàng.
Cho đường tròn (O;R) có đường kính AB. Từ điểm C nằm ngoài (O) kẻ cát tuyến CNM vuông góc với AB tại H (H nằm giữa O và B); AC cắt đường tròn (O;R) tại điểm K khác A, hai dây MN và BK cắt nhau ở E
a) CM: tứ giác AHEK nội tiếp đường tròn
b) Qua N kẻ đường thẳng vuông góc với AC cắt tia MK tại F. Chứng minh: tam giác NKF cân
Cho điểm A nằm ngoài đường tròn (O).Từ A kẻ hai tiếp tuyến AB,AC và cát tuyến ADE tới đường tròn (B,C là hai tiếp điểm;D nằm giữa A&E).Gọi H là giao điểm của AO và BC
a,Chứng minh rằng :ABOC là tứ giác nội tiếp
b,Chứng minh rằng :AH.AO=AD.AE
c,Tiếp tuyến tại D của đường tròn (O)cắt AB,AC theo thứ tự tại I và K.Qua điểm O kẻ đường thẳng vuông góc với OA cắt tia AB tại P và cắt tia AC tại Q.Chứng minh rằng IP+KQ>=PQ
Cho điểm A nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến AB, AC với (O) (B và C là các tiếp điểm). Vẽ đường kính CE của (O). Gọi H là giao điểm của OA và BC. a) Chứng minh tứ giác ABOC nội tiếp và BE // OA. b) AE cắt (O) tại D (khác E), BD cắt OA tại M. Chứng minh MAD MBA vàAH AC D D . c) Vẽ EI vuông góc với OA tại I; vẽ DK là đường kính của (O). Chứng minh 3 điểm K, I, B thẳng hàng.
Cho (O; R) và một điểm A nằm ngoài (O) sao cho OA = 2R. Từ A vẽ tiếp tuyến AB của (O) (B là tiếp điểm)
a) Chứng minh tam giác ABO vuông tại B và tính độ dài AB theo R.
b) Từ B kẻ dây cung BC của (O) vuông góc với cạnh OA tại H. chứng minh AC là tiếp tuyến của (O)
c) Chứng minh tam giác ABC đều
d) Từ H kẻ đường thẳng vuông góc với AB tại D. Đường tròn đường kính AC cắt cạnh DC tại E. Gọi F là trung điểm của OB. Chứng minh ba điểm A, E, F thẳng hàng.
Cho đường tròn (O; R) và một điểm A nằm ngoài đường tròn. Từ A vẽ hai tiếp tuyến AB và AC (B, C là tiếp điểm). Kẻ đường kính BD, đường thẳng vuông góc với BD tại O cắt đường thẳng DC tại E.
a) Chứng minh và DC // OA.
b) Chứng minh tứ giác AEDO là hình bình hành.
c) Đường thẳng BC cắt OA và OE lần lượt tại I và K. Chứng minh
MN giúp mình bài này với