Từ đẳng thức đã cho, lấy đạo hàm hai vế ta được: - 5 x 6 = f(t)
Do đó y = - 5 x 6
Đáp án C
Từ đẳng thức đã cho, lấy đạo hàm hai vế ta được: - 5 x 6 = f(t)
Do đó y = - 5 x 6
Đáp án C
Cho hàm số y = f(x) có đổ thị như hình vẽ bên. Biết rằng f(x) là một trong bốn hàm số được đưa ra trong các phương án A, B, C, D dưới đây. Tìm f(x)
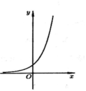
A . f ( x ) = e x
B . f ( x ) = ( 3 π ) x
C . f ( x ) = ln x
D . f ( x ) = x e π
Cho hàm số y=f(x) được xác định trên R và hàm số f=f’(x) có đồ thị như hình vẽ.
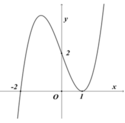
Tìm khoảng nghịch biến của hàm số y = f ( x 2 – 3 ) ?
A. (-∞;-1) và (0;1)
B. (-1;0)
C. (-1;0)
D. (-1;1)
Biết rằng đồ thị hàm số bậc 4: y = f(x) được cho như hình vẽ sau:
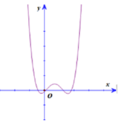
Tìm số giao điểm của đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) và trục Ox
A. 0
B. 2
C. 4
D. 6
Biết đồ thị hàm số bậc bốn y=f(x) được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ thị hàm số y=g(x)= [f’(x)]2 – f(x). f’’(x) và trục hoành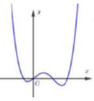
A. 4
B. 0.
C. 6.
D. 2.
Giả sử hàm số y = f ( x ) có đạo hàm là hàm số y=f'(x) có đồ thị được cho như hình vẽ dưới đây và f 0 + f 1 - 2 f 2 = f 4 - f 3 Tìm giá trị nhỏ nhất m của hàm số y = f ( x ) trên [0;4].
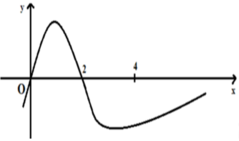
A. m = f 4
B. m = f 0
C. m = f 2
D. m = f 1
Cho hàm số y=f(x) liên tục và có đạo hàm trên R. Biết hàm số f’(x) có đồ thị được cho trong hình vẽ. Tìm điều kiện của m để hàm số g(x)=f(2019)x – mx +2 đồng biến trên [0;1]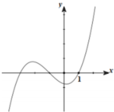
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: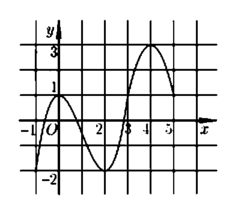
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Cho hàm số y=f(x) có đạo hàm f ’ ( x ) = x ( x - 1 ) 2 ( x - 2 ) . Tìm khoảng nghịch biến của đồ thị hàm số y=f(x)
A. (∞;0) và (1;2)
B. (0;1)
C. (0;2)
D. (2;+∞)
Cho hàm số y=f(x) có đồ thị đạo hàm y=f’(x) được cho như hình vẽ bên và các mệnh đề sau:
(1). Hàm số y=f(x) có duy nhất 1 điểm cực trị
(2). Hàm số y=f(x) nghịch biến trên khoảng (-2;1)
(3). Hàm số y=f(x) đồng biến trên khoảng 0 ; + ∞
(4). Hàm số g x = f x + x 2 có 2 điểm cực trị.
Số mệnh đề đúng là
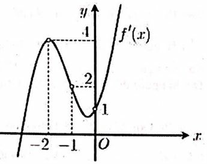
A. 1
B. 3
C. 4
D. 2