Chọn A.
Gọi z1; z2 là hai nghiệm của phương trình.
Theo Viet, ta có: 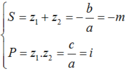
![]()
Ta có: m2 - 2i = - 4i khi và chỉ khi m2 = -2i hay m = ±( 1 - i)
Chọn A.
Gọi z1; z2 là hai nghiệm của phương trình.
Theo Viet, ta có: 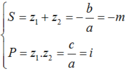
![]()
Ta có: m2 - 2i = - 4i khi và chỉ khi m2 = -2i hay m = ±( 1 - i)
Trong tập số phức, giá trị của m để phương trình bậc hai z 2 + m z + i = 0 có tổng bình phương hai nghiệm bằng -4i là:
A. ±(1 - i)
B. (1 - i)
C. ±(1 + i)
D. -1 - i
Giá trị của các số thực b, c để phương trình z 2 + b z + c = 0 nhận số phức z = 1 + i làm một nghiệm là:
A. b = 2 c = - 2
B. b = - 2 c = - 2
C. b = - 2 c = 2
D. b = 2 c = 2
Giá trị của các số thực b ; c để phương trình z2 + bz + c = 0 nhận số phức z =1 + i làm một nghiệm là:
A. 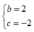
B. 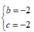
C. 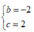
D. 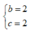
Cho phương trình z 2 + m z - 6 i = 0 . Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng m = ± ( a + b i ) ( a , b ∈ R ) . Giá trị a + 2 b là:
A. 0
B. 1
C. -2
D. -1
Cho phương trình z 2 + m z - 6 i = 0 . Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng m = ± ( a + b i ) ( a , b ∈ R ) . Giá trị a + 2 b là:
A. 0
B. 1
C. -2
D. -1
Cho phương trình z 2 + m z - 6 i = 0 . Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng m = ± ( a + b i ) ( a , b ∈ R ) . G i á t r ị a + 2 b là:
A. 0
B. 1
C. -1
D. –2
Cho phương trình z2 + mz - 6i = 0 Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng m = ± ( a + bi). Giá trị a + 2b là:
A. 0
B. 1
C.- 2
D. - 1
Trong tập các số phức, cho phương trình z 2 - 6 z + m = 1 Gọi m 0 là một giá trị của m để phương trình (1) có hai nghiệm phân biệt z 1 , z 2 thỏa mãn z 1 z 1 = z 2 z 2 Hỏi trong khoảng (0;20) có bao nhiêu giá trị m ?
A. 13
B. 11
C. 12
D. 10
Trong tập các số phức, cho phương trình z 2 - 6 z + m = 1 , m ∈ ℝ (1). Gọi m 0 là một giá trị của m để phương trình (1) có hai nghiệm phân biệt z 1 , z 2 thỏa mãn z 1 z 1 ¯ = z 2 z 2 ¯ Hỏi trong khoảng (0;20) có bao nhiêu giá trị m ?
A. 13
B. 11
C. 12
D. 10