Các câu hỏi tương tự
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R 1 được gọi là nửa đường tròn đơn vị (h.2.2). Nếu cho trước một góc nhọn α thì ta có thể xác định một điểm M duy nhất trên nửa đường tròn đơn vị sao cho ∠(xOM) α. Giả sử điểm M có tọa độ (xo; yo).Hãy chứng tỏ rằng sinα yo, cosα xo, tanα yo/xo , cotα xo/yo .
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R = 1 được gọi là nửa đường tròn đơn vị (h.2.2). Nếu cho trước một góc nhọn α thì ta có thể xác định một điểm M duy nhất trên nửa đường tròn đơn vị sao cho ∠(xOM) = α. Giả sử điểm M có tọa độ (xo; yo).
Hãy chứng tỏ rằng sinα = yo, cosα = xo, tanα = yo/xo , cotα = xo/yo .
Trong mặt phẳng tọa độ $Oxy$, cho elip $\left( E \right):\dfrac{{ x^2}}{4}+{{y}^2}=1.$ Gọi ${{F}_{1}};{{F}_2}$ là hai tiêu điểm của $\left( E \right)$ và điểm $M\in \left( E \right)$ sao cho $M{{F}_{1}}\bot M{{F}_2}$. Tính $M{{F}_{1}}^2+M{{F}_2}^2$ và diện tích $\Delta M{{F}_{1}}{{F}_2}.$
Trong mặt phẳng với hệ trục tọa độ $Oxy$, viết phương trình chính tắc của elip $left( E right)$ biết:
a) $left( E right)$ đi qua điểm $Mleft( dfrac{3}{sqrt{5}},;,dfrac{4}{sqrt{5}} right)$ và $M$ nhìn hai tiêu điểm ${{F}_{1}}$, ${{F}_2}$ dưới một góc vuông.
b) $left( E right)$ có độ dài trục lớn bằng $4sqrt2$, các đỉnh trên trục nhỏ và các tiêu điểm của $left( E right)$ cùng nằm trên một đường tròn.
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ $Oxy$, viết phương trình chính tắc của elip $\left( E \right)$ biết:
a) $\left( E \right)$ đi qua điểm $M\left( \dfrac{3}{\sqrt{5}}\,;\,\dfrac{4}{\sqrt{5}} \right)$ và $M$ nhìn hai tiêu điểm ${{F}_{1}}$, ${{F}_2}$ dưới một góc vuông.
b) $\left( E \right)$ có độ dài trục lớn bằng $4\sqrt2$, các đỉnh trên trục nhỏ và các tiêu điểm của $\left( E \right)$ cùng nằm trên một đường tròn.
tính F=\(\sin^2\dfrac{\pi}{6}+\sin^2\dfrac{2\pi}{6}+...+\sin^2\dfrac{5\pi}{6}+\sin^2\pi\)
2/ biết \(\sin\beta=\dfrac{4}{5},0< \beta< \dfrac{\pi}{2}\) giá trị của biểu thúc a=\(\dfrac{\sqrt{3}\sin\left(\alpha+\beta\right)-\dfrac{4\cos\left(\alpha+\beta\right)}{\sqrt{3}}}{\sin\alpha}\)
Trong mặt phẳng với hệ trục tọa độ $Oxy$, cho elip $\left( E \right)$ có phương trình: $\dfrac{{ x^2}}{9}+\dfrac{{{y}^2}}{4}=1$. Gọi ${{F}_{1}}, \, {{F}_2}$ là hai tiêu điểm của $\left( E \right)$. Tìm điểm $M$thuộc $\left( E \right)$ sao cho góc $\widehat{{{F}_{1}}M{{F}_2}}$ bằng ${{90}^{\circ}}$.
1.chứng minh hệ thức: dfrac{sinalpha+sin3alpha+sin5alpha}{cosalpha+cos3alpha+cos5alpha}tan3alpha2.rút gọn biểu thức: dfrac{1+sin4alpha-cos4alpha}{1+cos4alpha+sin4alpha}3. Tính 96sqrt{3}sindfrac{pi}{48}cosdfrac{pi}{48}cosdfrac{pi}{24}cosdfrac{pi}{12}cosdfrac{pi}{6}4. chứng minh rằng trong một △ABC ta có: tanA + tanB + tanC tanA tanB tanC (A,B,C cùng khác dfrac{pi}{2})
Đọc tiếp
1.\(\)chứng minh hệ thức: \(\dfrac{sin\alpha+sin3\alpha+sin5\alpha}{cos\alpha+cos3\alpha+cos5\alpha}=tan3\alpha\)
2.rút gọn biểu thức: \(\dfrac{1+sin4\alpha-cos4\alpha}{1+cos4\alpha+sin4\alpha}\)
3. Tính \(96\sqrt{3}sin\dfrac{\pi}{48}cos\dfrac{\pi}{48}cos\dfrac{\pi}{24}cos\dfrac{\pi}{12}cos\dfrac{\pi}{6}\)
4. chứng minh rằng trong một △ABC ta có:
tanA + tanB + tanC = tanA tanB tanC (A,B,C cùng khác \(\dfrac{\pi}{2}\))
giúp em câu này với ạ ;-;câu 1: tìm tất cả các giá trị của tham số m để phương trình dfrac{x}{sqrt{1-x^2}}dfrac{5-2m}{sqrt{1-x^2}} có nghiệmcâu 2: cho tanαdfrac{-2}{3}. Khi đó biểu thức M dfrac{sinalpha.cosalpha}{sin^2alpha-cos^2alpha}có giá trị bằng bao nhiêu ?em cảm ơn nhiều nhiều lắm luônnn :
Đọc tiếp
giúp em câu này với ạ ;-;
câu 1: tìm tất cả các giá trị của tham số m để phương trình \(\dfrac{x}{\sqrt{1-x^2}}=\dfrac{5-2m}{\sqrt{1-x^2}}\) có nghiệm
câu 2: cho tanα=\(\dfrac{-2}{3}\). Khi đó biểu thức M = \(\dfrac{sin\alpha.cos\alpha}{sin^2\alpha-cos^2\alpha}\)có giá trị bằng bao nhiêu ?
em cảm ơn nhiều nhiều lắm luônnn :>>
cho cos α=\(\dfrac{1}{3}\).khi đó giá trị biểu thức B=sin\(\left(\alpha-\dfrac{\Pi}{4}\right)-cos\left(\alpha-\dfrac{\Pi}{4}\right)\)
Trong mặt phẳng với hệ tọa độ Oxy. Cho đường tròn (C) : x2+ y2- 4x -2y -1 0 và đường thẳng d: x+ y+1 0. Tìm những điểm M thuộc đường thẳng d sao cho từ điểm M kẻ được đến (C) hai tiếp tuyến hợp với nhau góc 900.
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy. Cho đường tròn (C) : x2+ y2- 4x -2y -1= 0 và đường thẳng d: x+ y+1= 0. Tìm những điểm M thuộc đường thẳng d sao cho từ điểm M kẻ được đến (C) hai tiếp tuyến hợp với nhau góc 900.
![]()
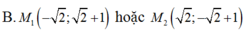
![]()
![]()
trong hệ tọa độ Oxy, cho hai điểm M(2;2) N(-1;-1) và đường thẳng (d) \(\left\{{}\begin{matrix}x=-8+2t\\y=t\end{matrix}\right.\) (t thuộc R ) tìm tọa độ điểm P nằm trên đường thẳng (d) sao cho tam giác MNP có diện tích bằng 18, biết điểm P (a;b) có tung độ âm. Tính giá trị 2a - 13b.












