a: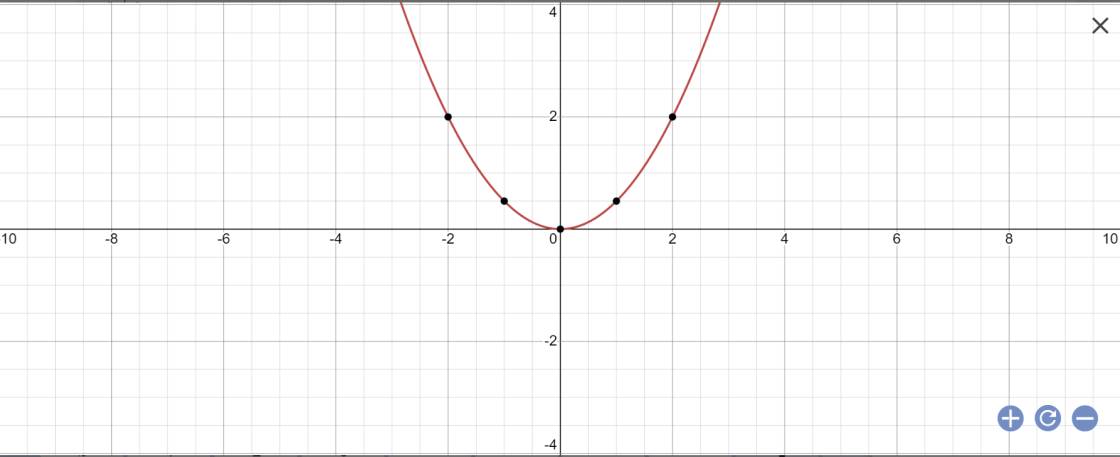 
b: PTHĐGĐ là:
1/2x^2-mx+m-1=0
Δ=(-m)^2-4*2(m-1)
=m^2-2m+2
=(m-1)^2+1>0 với mọi m
=>(d) luôn cắt (P) tại hai điểm phân biệt
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
trong mặt phẳng tọa độ oxy cho parabol (p) y=x^2/2 và đường thẳng (d) có phương trình y = mx-m+2
a) chứng minh rằng với mọi m , (d) lun cắt (P) tại 2 điểm A,B phân biệt . giả sử tọa độ của 2 điểm A,B là (x1;y1) và (x2;y2) . cm y1+y2 >= (2\(\sqrt{2}\) -1)(x1+x2)
Tìm tham số m để đường thẳng d: y mx + m + 1 và parabol (P):
y
x
2
cắt nhau tại hai điểm phân biệt có tọa độ
(
x
1
;
y
1
)
;
(
x
2
;
y
2
)
thỏa mãn
y
1...
Đọc tiếp
Tìm tham số m để đường thẳng d: y = mx + m + 1 và parabol (P): y = x 2 cắt nhau tại hai điểm phân biệt có tọa độ ( x 1 ; y 1 ) ; ( x 2 ; y 2 ) thỏa mãn y 1 + y 2 > 5
A. m >3 hoặc m< -1
B. m >-3 hoặc m >1
C. −3 < m < 1
D. m< -3 hoặc m >1
Trong mặt phẳng tọa độ Oxy, cho (P): y=x2 và đường thẳng (d): y=2x+4m2-8m+3 (m là tham số thực). Tìm các giá trị của m để (P) và (d) cắt nhau tại 2 điểm phân biệt A(x1,y1), B(x2,y2) thỏa mãn điều kiện y1+y2=10
Trong mặt phẳng Oxy Cho đường cong parabol (P) :y = 1/2 x bình và đường thẳng d : y = mx - 2m + 3 m là tham số thực
a /vẽ đồ thị hàm số của P
B/ tìm m để P và D cắt nhau tại 2 điểm phân biệt A (x1;y1) , B (x2;y2) thỏi hệ thức x1y2 + x2y1= -2
Trong mặt phẳng với hệ tọa độ Oxy Cho parabol p : y = 1/2x bình và đường thẳng d :y =( 2 m + 1) x - 2m bình - 2 m + 4( m là tham số thực )
a/ vẽ đồ thị hàm số P và d trên cùng một tọa độ khi m = 0
b/ tìm các giá trị của m để d cắt P tại 2 điểm phân biệt M (x1;y2) , N (x2;y2) sao cho biểu thức T = 2( y 1 + y2) - 3( x1 + x2 )- x1x2 đạt giá trị nhỏ nhất
Có bao nhiêu giá trị nguyên của tham số m để đường thẳng d: y 2mx – 2m + 3 và parabol (P)
y
x
2
cắt nhau tại hai điểm phân biệt có tọa độ
(
x
1
;
y
1
)
;
(
x
2
;
y
2
)
thỏa mãn...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để đường thẳng d: y = 2mx – 2m + 3 và parabol (P) y = x 2 cắt nhau tại hai điểm phân biệt có tọa độ ( x 1 ; y 1 ) ; ( x 2 ; y 2 ) thỏa mãn y 1 + y 2 < 9
A. 1
B. 3
C. 2
D. 0
trong mặt phẳng tọa độ Oxy, cho (P): y=x2 và đường thẳng (d): y=mx+8
a) Chứng minh (d) luôn cắt (P) tại 2 điểm phân biệt có hoành độ là x1 và x2 với mọi giá trị của m
b) Tìm tất cả các giá trị của m để x1 + √x2 = 0
MỜI CÁC CAO NHÂN Ạ!!!
Tìm tất cả các giá trị của tham số m sao cho parabol (P): y x2 cắt đường thẳng d: y mx – 2 tại 2 điểm phân biệt A(x1;y1) và B(x2;y2) thỏa mãn
y
1
+
y
2
2
(
x
1
+
x
2
)
−
1
Đọc tiếp
Tìm tất cả các giá trị của tham số m sao cho parabol (P): y = x2 cắt đường thẳng d: y = mx – 2 tại 2 điểm phân biệt A(x1;y1) và B(x2;y2) thỏa mãn y 1 + y 2 = 2 ( x 1 + x 2 ) − 1
chứng minh rằng với mọi giá trị của tham số m thì đường thẳng (d) : y = mx +1 luôn cắt Parabol (P) : y = x^2 tại hai điểm phân biệt. khi đó tìm m để y1 + y2 +y1*y2 = 7, với y1 , y2 là tung đọ của các giao điểm .
Trong mặt phẳng tọa độ Oxy, cho Parabol (P): y=x2 và đường thẳng (d): y=mx+5.
CMR:Với mọi giá trị của tham số m, đường thẳng (d) luôn cắt (P) tại 2 điểm phân biệt có hoành độ x1,x2.Tìm m để x12-9-mx2