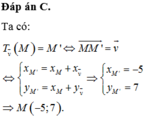Các câu hỏi tương tự
Trong mặt phẳng tọa độ Oxy, biết điểm M’(-3;0) là ảnh của điểm M(1;-2) qua phép tịnh tiến theo vectơ
u
→
và M”(2;3) là ảnh của điểm M’ qua phép tịnh tiến theo vectơ
v
→
. Tìm tọa độ vectơ
u
→
+
v
→
. A. (1;5) B. (-4;2) C. (5;3) D. (0;1)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, biết điểm M’(-3;0) là ảnh của điểm M(1;-2) qua phép tịnh tiến theo vectơ u → và M”(2;3) là ảnh của điểm M’ qua phép tịnh tiến theo vectơ v → . Tìm tọa độ vectơ u → + v → .
A. (1;5)
B. (-4;2)
C. (5;3)
D. (0;1)
Trong mặt phẳng với hệ tọa độ
O
x
y
cho điểm
A
(
0
;
1
)
và đường thẳng
d
có phương trình
x
2
+
2
t
y...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ O x y cho điểm A ( 0 ; 1 ) và đường thẳng d có phương trình x = 2 + 2 t y = 3 + t .Tìm điểm M thuộc d biết M có hoành độ âm và cách điểm A một khoảng bằng 5.
A. M ( 4 ; 4 )
B. M ( - 24 5 ; - 2 5 )
C. 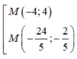
D. M ( - 4 ; 4 )
Trong khôn gian với hệ trục tọa độ Oxyz, cho mặt cầu
S
:
x
2
+
y
−
4
2
+
z
2
5
. Tìm tọa độ điểm A thuộc trục Oy, biết rằng ba mặt phẳng phân biệt qua A có các vec-tơ pháp tuyến lần lượt là các vec-tơ đơn vị của các trục tọa độ cắt mặt cầu theo thiết diện l...
Đọc tiếp
Trong khôn gian với hệ trục tọa độ Oxyz, cho mặt cầu S : x 2 + y − 4 2 + z 2 = 5 . Tìm tọa độ điểm A thuộc trục Oy, biết rằng ba mặt phẳng phân biệt qua A có các vec-tơ pháp tuyến lần lượt là các vec-tơ đơn vị của các trục tọa độ cắt mặt cầu theo thiết diện là ba hình tròn có tổng diện tích là 11 π
A. A 0 ; 2 ; 0 A 0 ; 6 ; 0
B. A 0 ; 0 ; 0 A 0 ; 8 ; 0
C. A 0 ; 0 ; 0 A 0 ; 6 ; 0
D. A 0 ; 2 ; 0 A 0 ; 8 ; 0
Trong không gian với hệ tọa độ Oxyz, cho (α) là mặt phẳng đi qua điểm M(1; - 2; 4) và có véc-tơ pháp tuyến (2; 3; 5). Phương trình mặt phẳng (α) là: A. 2x + 3y + 5z - 160 B. x - 2y + 4z - 160 C. 2x + 3y + 5z + 160 D. x - 2y + 4z0.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho (α) là mặt phẳng đi qua điểm M(1; - 2; 4) và có véc-tơ pháp tuyến ![]() =(2; 3; 5). Phương trình mặt phẳng (α) là:
=(2; 3; 5). Phương trình mặt phẳng (α) là:
A. 2x + 3y + 5z - 16=0
B. x - 2y + 4z - 16=0
C. 2x + 3y + 5z + 16=0
D. x - 2y + 4z=0.
Cho điểm M (1; 2; 5), mặt phẳng (P) đi qua điểm M cắt trục tọa độ Ox; Oy; Oz tại A, B, C sao cho M là trực tâm của tam giác ABC. Phương trình mặt phẳng (P) là
Đọc tiếp
Cho điểm M (1; 2; 5), mặt phẳng (P) đi qua điểm M cắt trục tọa độ Ox; Oy; Oz tại A, B, C sao cho M là trực tâm của tam giác ABC. Phương trình mặt phẳng (P) là
![]()
![]()
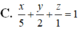
![]()
Trong không gian với hệ tọa độ Oxyz cho điểm M (-1;2;3). Khi đó điểm
M
đối xứng với M qua mặt phẳng (Oxy) có tọa độ là A.
M
(1;2;3) B.
M
(-1;-2;3) C.
M
(-1;2;-3) D.
M
(1;-2;3)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho điểm M (-1;2;3).
Khi đó điểm M ' đối xứng với M qua mặt phẳng (Oxy) có tọa độ là
A. M ' (1;2;3)
B. M ' (-1;-2;3)
C. M ' (-1;2;-3)
D. M ' (1;-2;3)
Cho M(2;-5;7) Tìm tọa độ điểm đối xứng của M qua mặt phẳng Oxy
A. M'(2;5;7)
B. M'(-2;5;7)
C. M'(-2;5;-7)
D. M'(2;-5;-7)
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(1;2; –3), B(–1;1;2), C(0;–3;–5). Xác định điểm M trên mặt phẳng Oxy sao cho:
M
A
→
+
M
B
→
+
M
C
→
đạt g...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(1;2; –3), B(–1;1;2), C(0;–3;–5). Xác định điểm M trên mặt phẳng Oxy sao cho: M A → + M B → + M C → đạt giá trị nhỏ nhất. Giá trị nhỏ nhất đó là
A. 0
B. 5
C. 5
D. 6
Trong không gian với hệ tọa độ Oxyz, cho điểm M(-1;2;-5). Tính khoảng cách từ điểm M đến mặt phẳng (Oxy). A. √30 B. √5 C. 25 D. 5
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(-1;2;-5). Tính khoảng cách từ điểm M đến mặt phẳng (Oxy).
A. √30
B. √5
C. 25
D. 5