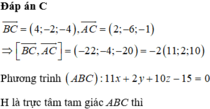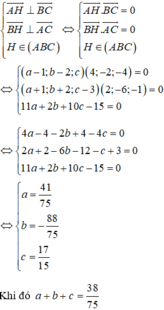Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(a;0;0), B(1;b;0), C(1;0;c), với a,b,c là các số thực thay đổi sao cho H(3;2;1) là trực tâm của tam giác ABC. Tính S=a+b+c.
A. S = 2
B. S = 19
C. S = 11
D. S = 9
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;-3;2), B(0;1;-2) và G(2;-1;1). Tọa độ điểm C sao cho tam giác ABC nhận G là trọng tâm là A.
C
1
;
-
1
;
2
3
B. C(3;-3;2) C. C(5;-1;2) D. C(1;1;0)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;-3;2), B(0;1;-2) và G(2;-1;1). Tọa độ điểm C sao cho tam giác ABC nhận G là trọng tâm là
A. C 1 ; - 1 ; 2 3
B. C(3;-3;2)
C. C(5;-1;2)
D. C(1;1;0)
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm
A
1
;
2
;
−
1
,
B
2
;
1
;
1
,
C
0
;
1
;
2
.
Gọi điểm...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A 1 ; 2 ; − 1 , B 2 ; 1 ; 1 , C 0 ; 1 ; 2 . Gọi điểm H x ; y ; z là trực tâm tam giác ABC. Giá trị của S = a + y + z là
A. 4
B. 6
C. 5
D. 7
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm
A
a
;
0
;
0
,
B
1
;
b
;
0
,
C
1
;
0
;
c
với a,b,c là các số thực thay đổi sao cho
H
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A a ; 0 ; 0 , B 1 ; b ; 0 , C 1 ; 0 ; c với a,b,c là các số thực thay đổi sao cho H 3 ; 2 ; 1 là trực tâm của tam giác ABC. Tính A - 1 ; - 1 ; 1
A. S = 2
B. S = 19
C. S = 11
D. S = 9
Trong không gian với hệ tọa độ Oxyz, cho điểm H(1;2;-3). Tìm phương trình mặt phẳng
α
cắt các trục tọa độ Ox, Oy, Oz lần lượt tại 3 điểm A, B, C sao cho H là trực tâm tam giác ABC. A.
α
: x+2y-3z-140 B.
α
: x+2y-3z+40 C.
α
: 6x+3y-2z-180 D.
α
: 6x+3y-2z+80
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm H(1;2;-3). Tìm phương trình mặt phẳng α cắt các trục tọa độ Ox, Oy, Oz lần lượt tại 3 điểm A, B, C sao cho H là trực tâm tam giác ABC.
A. α : x+2y-3z-14=0
B. α : x+2y-3z+4=0
C. α : 6x+3y-2z-18=0
D. α : 6x+3y-2z+8=0
Trong không gian với hệ trục tọa độ Oxyz cho A (1; 2; ‒1), B (‒2; 1; 0). Điểm
M
a
;
b
;
c
thuộc mặt phẳng
P
:
x
-
2
y
+
z
+
4
0
sao cho
M
A
M
B
11
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho A (1; 2; ‒1), B (‒2; 1; 0). Điểm M a ; b ; c thuộc mặt phẳng P : x - 2 y + z + 4 = 0 sao cho M A = M B = 11 2 . Khi đó giá trị của a bằng?
A. a = ± 1 2
B. a = 11 4
C. a = 1 2
D. a = - 1 2
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm
A
0
;
−
1
;
−
1
,
B
−
1
;
−
3
;
1
. Giả sử C,D là 2 điểm di động thuộc mặt phẳng
P...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A 0 ; − 1 ; − 1 , B − 1 ; − 3 ; 1 . Giả sử C,D là 2 điểm di động thuộc mặt phẳng P = 2 x + y − 2 z − 1 = 0 sao cho CD = 4 và A,C,D thẳng hàng. Gọi S 1 , S 2 lần lượt là diện tích lớn nhất và nhỏ nhất của tam giác BCD. Khi đó tổng S 1 + S 2 có giá trị bằng bao nhiêu?
A. 34 3
B. 17 3
C. 11 3
D. 37 3
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
Δ
:
x
-
1
1
y
2
z
+
1
-
1
và ba điểm A(3;2;-1), B(-3;-2;3), C(5;4;-7). Gọi tọa độ điểm M(a;b;c) nằm trên
Δ
sao cho MA+MB nhỏ nhất, khi đó giá trị...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ : x - 1 1 = y 2 = z + 1 - 1 và ba điểm A(3;2;-1), B(-3;-2;3), C(5;4;-7). Gọi tọa độ điểm M(a;b;c) nằm trên Δ sao cho MA+MB nhỏ nhất, khi đó giá trị của biểu thức P=a+b+c là:
A. P = 16 + 6 6 5
B. P = 42 - 6 6 5
C. P = 16 + 12 6 5
D. P = 16 - 6 6 5
Trong không gian với hệ tọa độ Oxyz, cho điểm H(1;2;-2). Gọi (P) là mặt phẳng đi qua H và cắt các trục Ox, Oy, Oz tại các điểm A, B, C sao cho H là trực tâm của tam giác ABC. Viết phương trình mặt cầu tâm O và tiếp xúc với mặt phẳng (P)? A.
x
2
+
y
2
+
z
2
81
B.
x
2
+
y
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm H(1;2;-2). Gọi (P) là mặt phẳng đi qua H và cắt các trục Ox, Oy, Oz tại các điểm A, B, C sao cho H là trực tâm của tam giác ABC. Viết phương trình mặt cầu tâm O và tiếp xúc với mặt phẳng (P)?
A. x 2 + y 2 + z 2 = 81
B. x 2 + y 2 + z 2 = 3
C. x 2 + y 2 + z 2 = 9
D. x 2 + y 2 + z 2 = 25