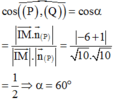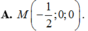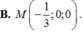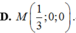Đáp án A.
Mặt phẳng (P) có VTPT 
Mặt cầu (S) có tâm 
Suy ra (Q) nhận
I
M
→
(
3
;
1
;
0
)
làm VTPT
suy ra góc giữa (P), (Q) và
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu S : x - 2 2 + y + 1 2 + z - 4 2 = 10 và mặt phẳng ( P ) : - 2 x + y + 5 z + 9 = 0 . Gọi mặt phẳng (Q) là tiếp diện của (S) tại M(5;0;4). Góc giữa mặt phẳng (P) và (Q).
A. 30 0 .
B. 45 0 .
C. 60 0 .
D. 90 0 .
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-4=0 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²=16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
A . M - 1 2 ; 0 ; 0
B . M - 1 3 ; 0 ; 0
C . M 1 ; 0 ; 0
D . M 1 3 ; 0 ; 0
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm nằm trên đường thẳng d : x 1 = y - 1 1 = z - 2 1 và tiếp xúc với hai mặt phẳng (P): 2x - z - 4 = 0, (Q): x – 2y – 2 = 0
A . S : x - 1 2 + y - 2 2 + z - 3 2 = 5
B . S : x - 1 2 + y - 2 2 + z - 3 2 = 5
C . S : x + 1 2 + y + 2 2 + z + 3 2 = 5
D . S : x - 1 2 + y - 2 2 + z - 3 2 = 3
Trong không gian với hệ trục tọa độ Oxyz , cho (P)là mặt phẳng qua đường thẳng d : x - 4 3 = y 1 = z + 4 - 4 và tiếp xúc với mặt cầu ( S ) : ( x - 3 ) 2 + ( y + 3 ) 2 + ( z - 1 ) 2 = 9 . Khi đó (P) song song với mặt phẳng nào sau đây?
Trong không gian Oxyz, cho điểm A ( 0 ; 1 ; 2 ) , mặt phẳng α : x - y + z - 4 = 0 và mặt cầu S : ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 16 . Gọi (P) là mặt phẳng đi qua A, vuông góc với α và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 2 2 = y - 1 = z 4 và mặt cầu (S): x - 1 2 + y - 2 2 + z - 1 2 = 2 . Hai mặt phẳng (P) và (Q) chứa d và tiếp xúc với (S).Gọi M và N là tiếp điểm. Độ dài đoạn MN bằng
A. 2 2
B. 4 3 3
C. 2 3 3
D. 4
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu
( S ) : x - 1 2 + y - 2 2 + z - 3 2 = 9 tâm I và mặt phẳng
(P): 2x + 2y -z + 24 =0.
Gọi H là hình chiếu vuông góc của I lên (P). Điểm M thuộc (S) sao cho đoạn MH có độ dài lớn nhất. Tính tọa độ điểm M.
A. M(-1;0;4)
B. M(0;1;2)
C. M(3;4;2)
D. M(4;1;2)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 2 2 = y - 1 = z 4 và mặt cầu S : x - 1 2 + y - 2 2 + z - 1 2 = 2 . Hai mặt phẳng (P), (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng?
A. 2 2
B . 4 3 3
C . 2 3 3
D. 4
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x + 6 y - 4 z - 2 = 0 mặt phẳng ( α ) : x + 4 y + z - 11 = 0 . Gọi (P) là mặt phẳng vuông góc với ( α ) , (P) song song với giá của vecto v → = ( 1 ; 6 ; 2 ) và (P) tiếp xúc với (S). Lập phương trình mặt phẳng ( P ).
A. 2x -y +2z -2 = 0 và x - 2y + z -21 = 0
B. x- 2y+ 2z + 3 = 0 và x - 2y + z -21 = 0
C. 2x -y +2z + 3 = 0 và 2x - y + 2z -21 = 0
D. 2x -y +2z + 5 = 0 và x - 2y + 2z -2 = 0
