Đáp án D
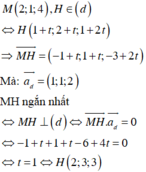
Bình luận: Nhận thấy ở các đáp án chỉ có điểm
H 2 ; 3 ; 3 ∈ d .
Đáp án D
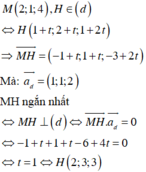
Bình luận: Nhận thấy ở các đáp án chỉ có điểm

H 2 ; 3 ; 3 ∈ d .
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : x = 1 − t y = 2 t z = 2 + 2 t , t ∈ ℝ và mặt phẳng P : x + y − z − 1 = 0 . Giao điểm M của d và (P) có tọa độ là
A. M 1 ; 1 ; 1
B. M 0 ; 2 ; 4
C. M 1 ; 0 ; 2
D. M 3 ; − 4 ; − 2
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(2; 1; 4) và đường thẳng △ : x = 1 + t y = 2 + t z = 1 + 2 t . Tìm điểm H thuộc △ sao cho MH nhỏ nhất
A. H ( 2 ; 3 ; 3 )
B. H ( 3 ; 4 ; 5 )
C. H ( 1 ; 2 ; 1 )
D. H ( 0 ; 1 ; - 1 )
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 1 = y - 2 1 = z - 1 2 , A(2 ;1 ;4). Gọi H(a ;b ;c) là điểm thuộc d sao cho AH có độ dài nhỏ nhất. Tính T = a 3 + b 3 + c 3
A. T=13
B. T = 5
C. T=8
D. T=62
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x+2y-z+16=0 và mặt cầu (s): (x-2)2 + (y+1)2 + (z-3)2=9. Điểm M di động trên trên (S) và điểm N di động trên (P) sao cho độ dài đoạn thẳng MN ngắn nhất. Tọa độ điểm M là
A. M(0;1;-1)
B. M(0;-3;4)
C. M(2;0;1)
D. M(-2;2;-3)
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và cho đường thẳng d có phương trình x - 2 2 = y + 2 - 1 = z - 3 1 . Tìm tọa độ của điểm B thuộc trục hoành sao cho AB vuông góc với d
A. B ( - 3 2 ; 0 ; 0 )
B. B ( 1 ; 0 ; 0 )
C. B ( 3 2 ; 0 ; 0 )
D. B ( 1 ; 0 ; 0 )
Trong không gian với hệ tọa độ Oxyz, phương trình của đường thẳng đi qua điểm M 2 ; − 1 ; 1 và vuông góc với hai đường thẳng d 1 : x 1 = y + 1 − 1 = z − 2 & d 2 : x = t y = 1 − 2 t z = 0 ( t ∈ ℝ ) là
A. x − 2 4 = y + 1 − 2 = z − 1 1 .
B. x + 2 4 = y + 3 2 = z 1 .
C. x − 2 3 = y + 1 2 = z − 1 − 1 .
D. x − 2 1 = y + 1 − 2 = z − 1 1 .
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) : x + y + z − 3 = 0 và đường thẳng Δ : x − 2 1 = y + 1 − 2 = z − 1 . Gọi I là giao điểm của ∆ và (P). Tìm điểm M thuộc (P) có hoành độ dương sao cho MI vuông góc với Δ v à M I = 4 14 .
A. M = ( 5 ; 9 ; − 11 )
B. M = ( 5 ; − 9 ; 11 )
C. M = ( − 5 ; 9 ; 11 )
D. M = ( 5 ; 9 ; 11 )
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x-y+z-10=0 và đường thẳng d: x + 2 2 = y - 1 1 = z - 1 - 1 . Đường thẳng Δ cắt (P) và d lần lượt tại M và N sao cho A(1;3;2) là trung điểm MN. Tính độ dài đoạn MN
A. MN=4 33
B. MN=2 26 , 5
C. MN=4 16 , 5
D. MN=2 33
Trong không gian với hệ tọa độ Oxyz, cho d là đường thẳng đi qua gốc tọa độ O, vuông góc với trục Ox và vuông góc với đường thẳng ∆ : x = 1 + t y = 2 - t z = 1 - 3 t . Phương trình của d là
A. x = t y = 3 t z = - t
B. x = t y = - 3 t z = - t
C. x 1 = y 3 = z - 1
D. x = 0 y = - 3 t z = t