Đáp án C.
Phương pháp:
Mặt phẳng P : A x + B y + C z + D = 0 có 1 VTPT là n → = A ; B ; C .
Cách giải:
P : x − 4 y + 3 z − 2 = 0 có một vecto pháp tuyến là n 3 → = − 1 ; 4 ; − 3 .
Đáp án C.
Phương pháp:
Mặt phẳng P : A x + B y + C z + D = 0 có 1 VTPT là n → = A ; B ; C .
Cách giải:
P : x − 4 y + 3 z − 2 = 0 có một vecto pháp tuyến là n 3 → = − 1 ; 4 ; − 3 .
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 = y + 1 2 = z - 2 1 và mặt phẳng P : 2 x - y - 2 z - 2 = 0 . (Q) là mặt phẳng chứa d và tạo với mặt phẳng (P) một góc nhỏ nhất. Gọi n Q → a ; b ; 1 là một vecto pháp tuyến của (Q). Đẳng thức nào đúng?
A. a - b = - 1
B. a + b = - 2
C. a - b = 1
D. a + b = 0
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 = y + 1 2 = z - 2 1 và mặt phẳng (P): 2x-y-2z-2=0. (Q) là mặt phẳng chứa d và tạo với mặt phẳng (P) một góc nhỏ nhất. Gọi n Q → a , b , 1 là một vecto pháp tuyến của (Q). Đẳng thức nào đúng?
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( P ) : x + y – z – 4 = 0 và điểm M (1;–2;-2). Tọa độ điểm N đối xứng với điểm M qua mặt phẳng (P) là
A. N (3;4;8)
B. N (3;0;–4)
C. N (3;0;8)
D. N (3;4;–4)
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) song song với hai đường thẳng d 1 : x - 2 2 = y + 1 - 3 = z 4 , d 2 : x = 2 + t y = 3 + 2 t z = 1 - t . Vecto nào sau đây là vecto pháp tuyến của mặt phẳng (P) ?
A. n ⇀ = ( 5 ; - 6 ; 7 )
B. n ⇀ = ( - 5 ; - 6 ; 7 )
C. n ⇀ = ( - 5 ; 6 ; - 7 )
D. n ⇀ = ( - 5 ; 6 ; 7 )
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : 3 x + 2 y − z + 1 = 0 . Mặt phẳng (P) có vecto pháp tuyến là
A. n → = − 1 ; 3 ; 2
B. n → = 3 ; − 1 ; 2
C. n → = 2 ; 3 ; − 1
D. n → = 3 ; 2 ; − 1
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x + y - z + 3 = 0 và đường thẳng d : x = 2 + m t y = n + 3 t z = 1 - 2 t . Với giá trị nào của m, n thì đường thẳng d nằm trong mặt phẳng (P)?
A. m = - 5 2 , n = 6
B. m = 5 2 , n = 6
C. m = 5 2 , n = - 6
D. m = - 5 2 , n = - 6
Trong không gian với hệ trục tọa độ Oxyz cho điểm A(2;0;-1) , mặt phẳng (P): 2x+y-z-2=0 và mặt phẳng (Q): x-3y-4=0. Gọi M là một điểm nằm trên (P) và N là điểm nằm trên (Q) sao cho A là trung điểm của MN. Khi M chạy trên mặt phẳng (P) thì quỹ tích điểm N là đường thẳng d có phương trình tương ứng là
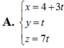
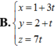
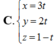
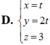
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-1;-2;2), B(-3;-2;0) và mặt phẳng (P):x+3y-z+2=0. Vectơ chỉ phương của đường thẳng d là giao tuyến của mặt phẳng (P) và mặt phẳng trung trực của đoạn AB có tọa độ là
A. u → = 1 ; - 1 ; 0
B. u → = 2 ; 3 ; - 1
C. u → = 1 ; - 2 ; 0
D. u → = 3 ; - 2 ; - 3
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) và đường thẳng d tương ứng có phương trình là 2 x - y + 3 z - 3 = 0 và x + 1 - 2 = y - 2 1 = z + 2 - 1 . Biết đường thẳng d cắt mặt phẳng (P) tại điểm M. Gọi N là điểm thuộc d sao cho M N = 3 , gọi K là hình chiếu vuông góc của điểm N trên mặt phẳng (P). Tính độ dài đoạn MK.
A. M K = 7 105
B. M K = 7 4 21
C. M K = 4 21 7
D. M K = 105 7