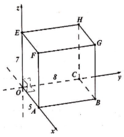
Gọi O và O' lần lượt là tâm của ABCD và A'B'C'D'
\(\Rightarrow O\) là trung điểm AC \(\Rightarrow O\left(\dfrac{1}{2};2;\dfrac{1}{2}\right)\)
O' là trung điểm B'D' \(\Rightarrow O'\left(\dfrac{1}{2};3;\dfrac{5}{2}\right)\)
\(\Rightarrow\overrightarrow{OO'}=\left(0,1,2\right)\)
Do ABCD.A'B'C'D' là hình hộp chữ nhật nên \(\overrightarrow{AA'}=\overrightarrow{OO'}\)
\(\Rightarrow\left\{{}\begin{matrix}x_{A'}+3=0\\y_{A'}-2=1\\z_{A'}-1=2\end{matrix}\right.\) \(\Rightarrow A'\left(-3,3,3\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{A'B'}=\left(1;-2;-2\right)\\\overrightarrow{AB}=\left(x_B+3;y_B-2;z_B-1\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_B+3=1\\y_B-2=-2\\z_B-1=-2\end{matrix}\right.\)
\(\Rightarrow B\left(-2;0;-1\right)\)
\(\overrightarrow{DD'}=\left(3-x_D;5-y_D;4-z_D\right)=\overrightarrow{OO'}\)
\(\Rightarrow\left\{{}\begin{matrix}3-x_D=0\\5-y_D=1\\4-z_D=2\end{matrix}\right.\) \(\Rightarrow D\left(3;4;2\right)\)