Chọn D
Gọi M (x;y;z).
Ta có MA = 2MB nên (x-1)²+ (y-2)²+ (z-3)² = 4 [ x²+ (y-4)²+ (z-5)² ]
![]()
Suy ra tập hợp các điểm M thỏa mãn MA = 2MB là mặt cầu (S) có tâm 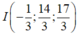 và bán kính
và bán kính ![]()
Vì 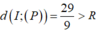 nên (P) không cắt (S).
nên (P) không cắt (S).
Do đó, khoảng cách từ điểm M đến mặt phẳng (P): 2x-2y-z+6 = 0 đạt giá trị nhỏ nhất là:
![]()



