Đáp án D
Gọi I(a; b; c) thỏa mãn
![]()
Khi đó
![]()
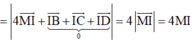
Suy ra MI min => M là hình chiếu của I trên (Oyz) => M(0;1;4)
Đáp án D
Gọi I(a; b; c) thỏa mãn
![]()
Khi đó
![]()
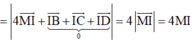
Suy ra MI min => M là hình chiếu của I trên (Oyz) => M(0;1;4)
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5) và D(3;3;3). Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức M A → + M B → + M C → + M D → đạt giá trị nhỏ nhất. Khi đó tọa độ của M là:
A. M (0;1;-4)
B. M (2;1;0)
C. M (0;1;-2)
D. M (0;1;4)
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(1;0;1), B(1;2;1), C(4;1;-2) và mặt phẳng P : x + y + z = 0 . Tìm trên (P) điểm M sao cho M A 2 + M B 2 + M C 2 đạt giá trị nhỏ nhất. Khi đó M có tọa độ:
A. M(1;1;-1)
B. M(1;1;1)
C. M(1;2;-1)
D. M(1;0;-1)
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; -2; -1), B (-2,-4,3), C (1;3;-1) và mặt phẳng (P): x + y -2z – 3 = 0. Tìm điểm M ∈ (P) sao cho M A → + M B → + 2 M C → đạt giá trị nhỏ nhất.
A . M 1 2 ; 1 2 ; - 1
B . M - 1 2 ; - 1 2 ; 1
C . M 2 ; 2 ; - 4
D . M - 2 ; - 2 ; 4
Trong không gian với hệ trục tọa độ Oxyz cho A (1; 2; ‒1), B (‒2; 1; 0). Điểm M (a; b; c) thuộc mặt phẳng sao cho . Khi đó giá trị của a bằng?
![]()
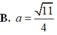
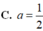

Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (1; 1; 2), B (-1; 0; 4), C (0; -1; 3) và điểm M thuộc mặt cầu (S): x2 + y2 + (z - 1)2 = 1. Khi biểu thức MA2 + MB2 + MC2 đạt giá trị nhỏ nhất thì độ đài đoạn AM bằng:
A. 2
B. 6
C. 6
D. 2
Trong không gian với hệ trục tọa độ Oxyz, cho A ( 3 ; − 1 ; − 3 ) , B ( − 3 ; 0 ; − 1 ) , C ( − 1 ; − 3 ; 1 ) và mặt phẳng ( P ) : 2 x + 4 y + 3 z − 19 = 0 . Tọa độ M ( a , b , c ) thuộc (P) sao cho M A → + 2 M B → + 5 M C → đạt giá trị nhỏ nhất. Khi đó a+b+c bằng:
A. 4
B. 5
C. 6
D. 7
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A (1;-2;0), B (-3;2;-4) và mặt phẳng (P): x + 2y + z - 3 = 0.
Gọi M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho tam giác
MAB cân tại M và có diện tích nhỏ nhất. Tính giá trị T = a 2 + b + c .
A. T = 1
B. T = 2
C. T = 0
D. T = 3
Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có A trùng với gốc tọa độ O, các đỉnh B (m; 0; 0), D (0; m; 0), A’ (0; 0; n) với m, n > 0 và m + n = 4. Gọi M là trung điểm của cạnh CC’. Khi đó thể tích tứ diện BDA’M đạt giá trị lớn nhất bằng:
A. 245/108
B. 9/4
C. 64/27
D. 75/32
Trong không gian với hệ tọa độ Oxyz, cho điểm M(4;1;9). Gọi (P) là mặt phẳng đi qua M và cắt 3 tia Ox, Oy, Oz lần lượt tại các điểm A,B,C (khác 0) sao cho (OA+OB+OC) đạt giá trị nhỏ nhất. Tính khoảng cách d từ điểm I(0;1;3) đến mặt phẳng (P).
A. d= 34 5
B. d= 36 5
C. d= 24 7
D. d= 30 7