Đáp án D
Áp dụng công thức trung điểm ta có

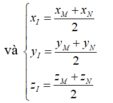
Suy ra
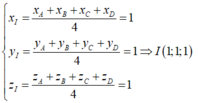
Đáp án D
Áp dụng công thức trung điểm ta có

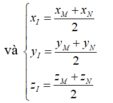
Suy ra
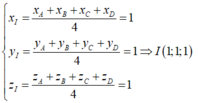
Trong không gian Oxyz. Cho điểm A ( 2 ; 0 ; 0 ) , B ( 0 ; 2 ; 0 ) , C ( 0 ; 0 ; 2 ) và D ( 2 ; 2 ; 2 ) . Gọi M, N lần lượt là trung điểm của AB và CD. Tọa độ trung điểm của đoạn MN là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho 4 điểm A( 2 ; 0 ; 0 ) , B( 0 ; 2 ; 0 ) , C( 0 ; 0 ; 2 ) , D( 2 ; 2 ; 2 ) . Gọi M, N lần lượt là trung điểm của AB và CD. Tọa độ trung điểm của đoạn thẳng MN là
![]()
![]()
![]()
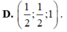
Trong không gian với hệ tọa độ Oxyz cho điểm A(2;0;0), B(0;2;0), C(0;0;2), D(2;2;2). Tính bán kính mặt cầu ngoại tiếp khối tứ diện ABCD.
A. 2 .
B. 2 2 .
C. 3 .
D. 2 3 .
Trong không gian Oxyz, cho bốn điểm A(1;2;-4), B(1;-3;1), C(2;2;3), D(1;0;4). Gọi (S) là mặt cầu đi qua bốn điểmA,B,C,D. Tọa độ tâm I và bán kính R mặt cầu (S) là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai điểm A ( 1 ; - 1 ; 2 ) và B ( 3 ; 1 ; 0 ) . Tọa độ trung điểm I của đoạn AB là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-3;2;-1), B(1;0;5). Tọa độ trung điểm I của đoạn thẳng AB là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x = 1 + t y = 2 z = 3 - t và điểm A(-1;2;-1). Tìm tọa độ điểm I là hình chiếu của I lên ∆
![]()
![]()
![]()
![]()
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)
CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)
CH 3. Trong không gian Oxyz cho 2 vectơ a =(1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8
CH 4.Trong không gian Oxyz cho 2 vecto a= (3; 1; 2) và b= (2; 0; -1); khi đó vectơ 2a-b có độ dài bằng : А. 3/5 В. 29 С. M D. S/5
CH 5. Cho hình bình hành ABCD với A (-1;0;2), B(3;4;0) D (5;2;6). Tìm khẳng định sai. A. Tâm của hình bình hành có tọa độ là (4;3;3) B. Vecto AB có tọa độ là (4;-4;-2) C. Tọa độ của điểm C là (9;6;4) D. Trọng tâm tam giác ABD có tọa độ là (3;2;2)
Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : x + 1 2 = y 1 = z - 2 1 mặt phẳng (P): x+y-2z+5=0 và A(1;-1;2) Đường thẳng ∆ cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN . Một vectơ chỉ phương của ∆ là:
A. u → = ( 2 ; 3 ; 2 )
B. u → = ( 1 ; - 1 ; 2 )
C. u → = ( - 3 ; 5 ; 1 )
D. u → = ( 4 ; 5 ; - 13 )