Chọn B.
Phương pháp:
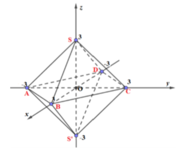
Hình đa diện được lập thành là hình bát diện đều.
Cách giải:

Chọn B.
Phương pháp:
Hình đa diện được lập thành là hình bát diện đều.
Cách giải:


Trong không gian với hệ tọa độ Oxyz, biết rằng tập hợp các điểm M x ; y ; z sao cho x + y + z = 3 là một hình đa diện. Tính thể tích V của khối đa diện đó
A. V = 54
B. V = 72
C. V = 36
D. V = 27
Tập hợp các điểm có tọa độ x ; y ; z sao cho 0 ≤ x ≤ 3 , − 1 ≤ y ≤ 5 , − 2 ≤ z ≤ 2 là tập hợp của một khối đa diện (lồi) có một tâm đối xứng. Tìm tọa độ tâm đối xứng đó.
A. 3 2 ; 3 ; 2
B. 2 ; 3 ; 2
C. − 1 ; 0 ; 2
D. 3 2 ; 2 ; 0
Tập hợp các điểm có tọa độ ( x ; y ; z ) sao cho 0 ≤ x ≤ 3 , - 1 ≤ y ≤ 5 , - 2 ≤ z ≤ 2 là tập hợp của một khối đa diện (lồi) có một tâm đối xứng. Tỉm tọa độ tâm đối xứng đó
A. ( - 1 ; 0 ; 2 )
B. ( 2 ; 3 ; 2 )
C. ( 3 2 ; 2 ; 0 )
D. ( 3 2 ; 3 ; 2 )
Trong không gian với hệ tọa độ Oxyz, cho hình chóp có đỉnh S ( 2 ; 3 ; 5 ) và đáy là một đa giác nằm trong mặt phẳng (P): 2 x + y - 2 z - 3 = 0 , có diện tích bằng 12. Tính thể tích của khối chóp đó.
A. 4
B. 24
C. 8
D. 72
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A ( a ; 0 ; 0 ) , B ( 0 ; b ; 0 ) , C ( 0 ; 0 ; c ) , trong đó a > 0 , b > 0 , c > 0 và 3 a + 1 b + 3 c = 5 . Biết mặt phẳng (ABC) tiếp xúc với mặt cầu (S) có phương trình là ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 3 ) 2 = 304 25 , khi đó thể tích của khối tứ diện OABC nằm trong khoảng nào?
A . ( 0 ; 1 2 ) .
B. (0;1).
C. (1;3).
D. (4;5).
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0;1;0), B(2;2;2), C(-2;3;1) và đường thẳng d : x - 1 2 = y + 2 - 1 = z - 3 2 . Tìm điểm M thuộc d để thể tích V của tứ diện MABC bằng 3.
A. M 1 - 15 2 ; 9 4 ; - 11 2 , M 2 - 3 2 ; - 3 4 ; 1 2
B. M 1 - 3 5 ; - 3 4 ; 1 2 , M 2 - 15 2 ; 9 4 ; 11 2
C. M 1 3 2 ; - 3 4 ; 1 2 , M 2 15 2 ; 9 4 ; 11 2
D. M 1 3 5 ; - 3 4 ; 1 2 , M 2 15 2 ; 9 4 ; 11 2
Trong không gian với hệ toạ độ Oxyz, cho hình lập phương giới hạn bởi các mặt phẳng x=0;y=0;z=0;x=10;y=10;z=10. Gọi S là tập hợp tất cả các điểm A(x;y;z),( x , y , z ∈ Z ) nằm bên trong (kể cả các mặt) của hình lập phương. Lấy ngẫu nhiên một điểm A(x;y;z) ∈ S. Xác suất để x<y và x<z bằng
A. 285 1331
B. 35 121
C. 204 1331
D. 57 200
Trong không gian với hệ tọa độ Oxyz, cho đường cong (T) là tập hợp tâm của các mặt cầu (S) đi qua điểm A(1;1;1) đồng thời tiếp xúc với hai mặt phẳng α : x + y + z − 6 = 0 và β : x + y + z + 6 = 0 . Diện tích hình phẳng giới hạn bởi đường cong (T) bằng
A. 3 5
B. 9 π
C. 48 π
D. 45 π
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 - 2 = y - 1 = z - 2 1 và hai điểm A(-1;3;1),B(0;2;-1). Tìm tọa độ điểm C thuộc d sao cho diện tích của tam giác ABC nhỏ nhất.
A . C ( - 1 ; 0 ; 2 )
B . C ( 1 ; 1 ; 1 )
C . C ( - 3 ; - 1 ; 3 )
D . C ( - 5 ; - 2 ; 4 )