Gọi A(a;0;0), B(0;b;0) ![]()
Vì ![]()
![]()
Khi đó
![]()
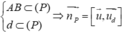 =(-1;-2;-5)
=(-1;-2;-5)
Và (P) đi qua điểm
![]()
Chọn đáp án C.
Gọi A(a;0;0), B(0;b;0) ![]()
Vì ![]()
![]()
Khi đó
![]()
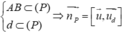 =(-1;-2;-5)
=(-1;-2;-5)
Và (P) đi qua điểm
![]()
Chọn đáp án C.
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;2;3) và đường thẳng (d): x - 2 2 = y + 2 - 1 = z - 3 1 . Gọi điểm B thuộc trục Ox sao cho AB vuông góc với đường thẳng (d). Khoảng cách từ B đến mặt phẳng ( α ): 2x+2y-z-1=0 là:
A. 2
B. 2 3
C. 1 3
D. 1
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng: △ : x 1 = y - 1 1 = z - 2 - 1 và mặt phẳng (P): x+2y+2z-4=0. Phương trình đường thẳng d nằm trong mặt phẳng (P) sao cho d cắt và vuông góc với đường thẳng Δ là
A. d : x = - 3 + t y = 1 - 2 t z = 1 - t
B. d : x = 3 t y = 2 + t z = 2 + 2 t
C. d : x = - 2 - 4 t y = - 1 + t z = 4 - t
D. d : x = - 1 - t y = 3 - 3 t z = 3 - 2 t
Trong không gian tọa độ Oxyz, cho đường thẳng x - 1 1 = y - 2 - 2 = z + 1 - 1 và mặt phẳng (P):2x - y - 2z - 2018 = 0. Phương trình mặt phẳng (Q) chứa đường thẳng D và tạo với (P) một góc nhỏ nhất cắt các trục tọa độ lần lượt tại các điểm A, B, C. Thể tích tứ diện O.ABC là:
A. 1 6
B. 32 3
C. 32 6
D. 64 3
Trong không gian với hệ tọa độ Oxyz, gọi d là giao tuyến của hai mặt phẳng có phương trình lần lượt là 2 x − 2 y − z = 0 và x + 3 y + z − 1 = 0 . Tính cosin của góc giữa đường thẳng d và trục Oy.
A. 3 35
B. 3 23
C. 3 74
D. 3 6
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x + 2 1 = y - 2 1 = z - 1 và mặt phẳng ( P ) : x + 2 y - 3 z + 4 = 0 . Đường thẳng d nằm trong (P) sao cho d cắt và vuông góc với ∆ có phương trình là:
A. x + 3 1 = y - 1 - 1 = z - 1 2
B. x + 1 - 1 = y - 3 2 = z + 1 1
C. x - 3 1 = y + 1 - 1 = z + 1 2
D. x + 3 - 1 = y - 1 2 = z - 1 1
Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng (P): x-2y+z-1=0;(Q): x-2y+z+8=0;(C): x-2y+z=0 Một đường thẳng d thay đổi cắt ba mặt phẳng (P), (Q), (R) lần lượt tại A, B, C. Tìm giá trị nhỏ nhất của T = A B 2 + 144 A C
A. 72 3 3
B. 96.
C. 108.
D. 72 4 3
Trong không gian với hệ trục tọa độ Oxyz, cho ba mặt phẳng P : x - 2 y + z - 1 = 0 , Q : x - 2 y + z + 8 = 0 và R : x - 2 y + z - 4 = 0 . Một đường thẳng d thay đổi cắt ba mặt phẳng (P), (Q), (R) lần lượt tại A, B, C. Tìm giá trị nhỏ nhất của biểu thức T = A B 2 + 144 A C
A. 72 3 3
B. 96.
C. 108.
D. 72 4 3
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : x + 2 y + z - 4 = 0 và đường thẳng d : x + 1 2 = y 1 = z + 2 3 . Viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d.
A. x - 1 5 = y - 1 - 1 = z - 1 - 3
B. x - 1 5 = y - 1 - 1 = z - 1 3
C. x - 1 5 = y - 1 1 = z - 1 - 3
D. x - 1 5 = y - 1 - 1 = z - 1 2
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 2 1 = y - 2 2 = z + 2 - 1 và mặt phẳng ( α ) :2x+2y-z-4=0. Tam giác ABC có A(-1;2;1), các đỉnh B, C nằm trên (α) và trọng tâm G nằm trên đường thẳng d. Tọa độ trung điểm M của BC là
A. M(2;1;2)
B. M(0;1;-2)
C. M(1;-1;-4)
D. M(2;-1;-2)