Các câu hỏi tương tự
Trong không gian Oxyz, cho mặt cầu (S):
(
x
-
5
)
2
+
(
y
-
1
)
2
+
(
z
+
2
)
2
3
có bán kính bằng A.
3
B.
2
3...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): ( x - 5 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 3 có bán kính bằng
A. 3
B. 2 3
C. 9
D. 3
Trong không gian hệ tọa độ Oxyz, cho mặt cầu (S):
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-
3
)
2
4
. Tìm tọa độ tâm I và bán kính R của mặt cầu đó A. I(-1;2;3), R2 B. I(-1;2;-3), R...
Đọc tiếp
Trong không gian hệ tọa độ Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 4 . Tìm tọa độ tâm I và bán kính R của mặt cầu đó
A. I(-1;2;3), R=2
B. I(-1;2;-3), R=4
C. I(1;-2;3); R=2
D. I(1;-2;3), R=4
Trong không gian Oxyz, cho hai đường thẳng
△
1
:
x
-
4
3
y
-
1
-
1
z
+
5
-
2...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng △ 1 : x - 4 3 = y - 1 - 1 = z + 5 - 2 và △ 2 : x - 2 = y + 3 = z 1 Trong tất cả các mặt cầu tiếp xúc với cả hai đường thẳng △ 1 và △ 2 Gọi (S) là mặt cầu có bán kính nhỏ nhất. Bán kính của mặt cầu (S) là
A. 12
B. 6
C. 24
D. 3
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-5)² + (y-1)² + (z+2)²9. Tính bán kính R của mặt cầu (S). A. R18 B. R9 C. R3 D. R6.
Đọc tiếp
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-5)² + (y-1)² + (z+2)²=9. Tính bán kính R của mặt cầu (S).
A. R=18
B. R=9
C. R=3
D. R=6.
Trong không gian tọa độ Oxyz, cho mặt cầu (S):
(
x
-
2
)
2
+
y
2
+
(
z
+
1
)
2
9
và mặt phẳng (P): 2x-y-2z-30. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho mặt cầu (S): ( x - 2 ) 2 + y 2 + ( z + 1 ) 2 = 9 và mặt phẳng (P): 2x-y-2z-3=0. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn (C). Tính bán kính R của (C)
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxyz, mặt cầu (S):
(
x
+
4
)
2
+
(
y
-
5
)
2
+
(
z
+
6
)
2
9
có tâm và bán kính là A. I(4;-5;6), R5 B. I(-4;5;-6), R81 C. I(4;-5;6) D. I(-4;5;-6),...
Đọc tiếp
Trong không gian tọa độ Oxyz, mặt cầu (S): ( x + 4 ) 2 + ( y - 5 ) 2 + ( z + 6 ) 2 = 9 có tâm và bán kính là
A. I(4;-5;6), R=5
B. I(-4;5;-6), R=81
C. I(4;-5;6)
D. I(-4;5;-6), R=3
Trong không gian Oxyz, cho điểm
A
(
0
;
1
;
2
)
, mặt phẳng
α
:
x
-
y
+
z
-
4
0
và mặt cầu
S
:
(
x
-
3...
Đọc tiếp
Trong không gian Oxyz, cho điểm A ( 0 ; 1 ; 2 ) , mặt phẳng α : x - y + z - 4 = 0 và mặt cầu S : ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 16 . Gọi (P) là mặt phẳng đi qua A, vuông góc với α và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
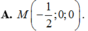
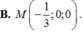
![]()
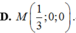
Trong không gian Oxyz, cho mặt cầu (S):
(
x
+
1
)
2
+
(
y
-
1
)
2
+
(
z
+
2
)
2
3
và hai đường thẳn...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 3 và hai đường thẳng d x : x - 2 1 = y 2 = z - 1 - 1 ; △ : x 1 = y 1 = z - 1 - 1 Phương trình nào dưới đây là phương trình mặt phẳng cắt mặt cầu (S) theo giao tuyến là một đường tròn (C) có bán kính bằng 1 và song song với d và △ .
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 25
Tìm tọa độ tâm I và bán kính R của mặt cầu (S)
A. I(1; -2; -3); R = 25
B. I(-1; 2; 3); R = 5
C. I(-1; 2; 3); R = 25
D. I(1; -2; -3); R = 5
Trong không gian tọa độ Oxyz, mặt cầu: (S):
(
x
+
4
)
2
+
(
y
-
5
)
2
+
(
z
+
6
)
2
9
có tâm và bán...
Đọc tiếp
Trong không gian tọa độ Oxyz, mặt cầu: (S): ( x + 4 ) 2 + ( y - 5 ) 2 + ( z + 6 ) 2 = 9 có tâm và bán kính lần lượt là
![]()
![]()
![]()
![]()




