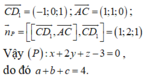Các câu hỏi tương tự
Trong hệ tục toạ độ không gian Oxyz, cho A(1;0;0), B(0;b;0), C(0;0;c), biết b,c 0, phương trình mặt phẳng
P
:
y
-
z
+
1
0
. Tính Mb+c biết
A
B
C
⊥
P
,
d
(
O
,
A
B
C
)...
Đọc tiếp
Trong hệ tục toạ độ không gian Oxyz, cho A(1;0;0), B(0;b;0), C(0;0;c), biết b,c > 0, phương trình mặt phẳng P : y - z + 1 = 0 . Tính M=b+c biết A B C ⊥ P , d ( O , A B C ) = 1 3
A. 2
B. 1 2
C. 5 2
D. 1
Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²25 và hai điểm A (3;-2;6), B (0;1;0). Mặt phẳng (P):ax+by+cz-20 chứa đường thẳng AB và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính giá trị của biểu thức M2a+b-c. A. M2. B. M3. C. M1. D. M4.
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=25 và hai điểm A (3;-2;6), B (0;1;0). Mặt phẳng (P):ax+by+cz-2=0 chứa đường thẳng AB và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính giá trị của biểu thức M=2a+b-c.
A. M=2.
B. M=3.
C. M=1.
D. M=4.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
−
2
1
y
+
1
1
z
+
1
−
2
và
Δ
:
x
−
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x − 2 1 = y + 1 1 = z + 1 − 2 và Δ : x − 3 1 = y + 1 1 = z + 3 2 . Viết phương trình mặt phẳng (P) chứa d và tạo với tam giác một góc 30 ° . có dạng x + a y + b z + c = 0 với a , b , c ∈ ℤ khi đó giá trị a+b+c là
A. 8
B. -8
C. 7
D. -7
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình: ax+by+cz-10 với c0 đi qua 2 điểm A(0;1;0), B(1;0;0) và tạo với (Oyz) một góc
60
°
. Khi đó a+b+c thuộc khoảng nào dưới đây? A. (5;8) B. (8;11) C. (0;3) D. (3;5)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình: ax+by+cz-1=0 với c<0 đi qua 2 điểm A(0;1;0), B(1;0;0) và tạo với (Oyz) một góc 60 ° . Khi đó a+b+c thuộc khoảng nào dưới đây?
A. (5;8)
B. (8;11)
C. (0;3)
D. (3;5)
Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23) và mặt cầu (S) có phương trình (S): (x - 5)2 + (
y
+
3
)2 + (z + 2)2 72. Mặt phẳng (P): x + by + cz + d 0 đi qua điểm A và tiếp xúc với mặt cầu (S) sao cho khoảng cách từ B đến mặt phẳng (P) lớn nhất. Giá trị của b + c + d khi đó là: A. b + c + d 2 B. b + c + d 4 C. b + c + d 3 D. b + c + d 1
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23) và mặt cầu (S) có phương trình (S): (x - 5)2 + ( y + 3 )2 + (z + 2)2 = 72. Mặt phẳng (P): x + by + cz + d = 0 đi qua điểm A và tiếp xúc với mặt cầu (S) sao cho khoảng cách từ B đến mặt phẳng (P) lớn nhất. Giá trị của b + c + d khi đó là:
A. b + c + d = 2
B. b + c + d = 4
C. b + c + d = 3
D. b + c + d = 1
Trong không gian Oxyz Cho A(0; 0; a), B(b; 0; 0), C(0; c; 0). Phương trình mặt phẳng (ABC) là:A.
x
a
+
y
b
+
z
c
1
B.
x
a
+...
Đọc tiếp
Trong không gian Oxyz Cho A(0; 0; a), B(b; 0; 0), C(0; c; 0). Phương trình mặt phẳng (ABC) là:
A. x a + y b + z c = 1 B. x a + y c + z b = 1
C. x b + y c + z a = 1 D. x c + y b + z a = 1
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
-
1
2
+
(
y
-
2
)
2
+
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + ( y - 2 ) 2 + z - 3 2 = 16 và các điểm A (1; 0; 2), B (-1; 2; 2). Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của (P) với mặt cầu (S) có diện tích nhỏ nhất.Khi viết phương trình (P) dưới dạng (P): ax + by + cz + 3 = 0. Tính T = a + b + c
A. 3
B. -3
C. 0
D. -2
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(3;-2;6),B(0;1;0) và mặt cầu (S):
(
x
-
1
)
2
+
(
y
-
2
)
2
+
(
z
-
3
)
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(3;-2;6),B(0;1;0) và mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 . Mặt phẳng (P): ax+by+cz-2=0 đi qua A và B và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T=a+b+c
A. T=3
B. T=5
C. T=2
D. T=4
Trong không gian Oxyz, biết mặt phẳng ax+by+cz-240 qua A(1;2;3) và vuông góc với hai mặt phẳng (P): 3x-2y+z+40, (Q): 5x-4y+3z+10. Giá trị a+b+c bằng A. 8. B. 9. C. 10. D. 12.
Đọc tiếp
Trong không gian Oxyz, biết mặt phẳng ax+by+cz-24=0 qua A(1;2;3) và vuông góc với hai mặt phẳng (P): 3x-2y+z+4=0, (Q): 5x-4y+3z+1=0. Giá trị a+b+c bằng
A. 8.
B. 9.
C. 10.
D. 12.