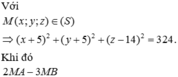
= 2 x + 14 2 + y - 13 2 + z + 4 2 - 3 x + 7 2 + y + 1 2 + z - 1 2 = 4 x + 14 2 + y - 13 2 + z + 4 2 + 5 x + 5 2 + y + 5 2 + z - 14 2 - 324 - 3 x + 7 2 + y + 1 2 + z - 1 2 = 3 x + 9 2 + y - 3 2 + z - 6 2 - x + 7 2 + y + 1 2 + z - 1 2


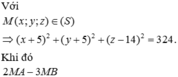
= 2 x + 14 2 + y - 13 2 + z + 4 2 - 3 x + 7 2 + y + 1 2 + z - 1 2 = 4 x + 14 2 + y - 13 2 + z + 4 2 + 5 x + 5 2 + y + 5 2 + z - 14 2 - 324 - 3 x + 7 2 + y + 1 2 + z - 1 2 = 3 x + 9 2 + y - 3 2 + z - 6 2 - x + 7 2 + y + 1 2 + z - 1 2


Trong không gian với hệ toại độ Oxyz, cho ba điểm A 1 ; 2 ; − 3 , B 2 ; 0 ; 1 , C 3 ; − 1 ; 1 . Gọi M là điểm di động trên mặt phẳng Oyz. Tìm giá trị nhỏ nhất của biểu thức P = 3 M B → + M C → + 2 M A → + 2 M B →
A. 42 6
B. 42
C. 3 82
D. 82 2
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng P : x - y + z + 3 = 0 , Q : x + 2 y - 2 z - 5 = 0 và mặt cầu S : x 2 + y 2 + z 2 - 2 z + 4 y - 6 z - 11 = 0 . Gọi M là điểm di động trên (P) sao cho MN luôn vuông góc với (Q). Giá trị lớn nhất của độ dài đoạn thẳng MN bằng
A. 9 + 5 3
B. 28
C. 14
D. 3 + 5 3
Trong không gian Oxyz cho mặt cầu ( S ) : x 2 + y - 3 2 + z + 4 2 = 4 Xét hai điểm M,N di động trên (S) sao cho MN=1 Giá trị nhỏ nhất của O M 2 - O N 2 bằng
A. - 10
B. - 4 - 3 5
C. - 5
D. - 6 - 2 5
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 4 và hai điểm A(-1;2;-3); B(5;2;3). Gọi M là điểm thay đổi trên mặt cầu (S). Tính giá trị lớn nhất của biểu thức 2 M A 2 + M B 2
A. 5
B. 123
C. 65
D. 112
Trong không gian Oxyz, cho mặt cầu S : x - 1 2 + y - 1 2 + z - 1 2 = 12 và mặt phẳng (P):x-2y+2z+11=0. Xét điểm M di động trên (P); các điểm A, B, C phân biệt di động trên (S) sao cho AM, BM, CM là các tiếp tuyến của (S). Mặt phẳng (ABC) luôn đi qua điểm cố định nào dưới đây?
A. 1 4 ; - 1 2 ; - 1 2
B. (0;-1;3)
C. 3 2 ; 0 ; 2
D. (0;3;-1)
Trong không gian Oxyz, cho ba điểm A(-1;3;5), B(2;6;-1), C(-4;-12;5) và mặt phẳng (P):x+2y-2z-5=0 Xét điểm M di động trên mặt phẳng (P) giá trị nhỏ nhất của biểu thức M A ⇀ - 4 M B ⇀ + M A ⇀ + M B ⇀ + M C ⇀ bằng
A. 6 29
B. 6 10
C. 18
D. 21
Trong không gian Oxyz, cho ba điểm A(0;0;4),B(3;2;6),C(3;-2;6). Gọi M là điểm di động trên mặt cầu (S): x 2 + y 2 + z 2 = 4 . Giá trị lớn nhất của biểu thức M A + | M B → + M C → | bằng
A. 24.
B. 30.
C. 22.
D. 26.
Trong không gian với hệ tọa độ Oxyz cho các điểm A 0 ; - 1 ; 3 , B - 2 ; - 8 ; - 4 , C 2 ; - 1 ; 1 và mặt cầu S : x - 1 2 + y - 2 2 + z - 3 2 = 14 . Gọi M x M ; y M ; z M là điểm trên S sao cho biểu thức 3 M A → - 2 M B → + M C → đạt giá trị nhỏ nhất. Tính P = x M + y M
A. P = 0
B. P = 14
C. P = 6
D. P = 3 14
Trong không gian Oxyz, cho mặt cầu ( S ) : x + 1 2 + y - 2 2 + z + 3 2 = 25 và điểm A(2;2;1). Xét các điểm B, C, D thay đổi thuộc (S) sao cho AB, AC, AD đôi một vuông góc nhau. Khoảng cách từ tâm của (S) đến mặt phẳng (BCD) có giá trị lớn nhất bằng
A. 10 3
B. 1
C. 5 6
D. 5 3