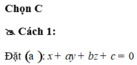
Ta có A B → = 2 ; 8 ; - 4 một vtpt của
mặt phẳng trung trực đoạn AB là
n → = ( 1 ; a ; b )
Gọi I là trung điểm của đoạn AB,
ta có I(2;1;0)
Đk để (a) là mp trung trực của đoạn
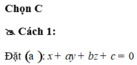
Ta có A B → = 2 ; 8 ; - 4 một vtpt của
mặt phẳng trung trực đoạn AB là
n → = ( 1 ; a ; b )
Gọi I là trung điểm của đoạn AB,
ta có I(2;1;0)
Đk để (a) là mp trung trực của đoạn
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A (1;-3;2), B (3;5;-2). Phương trình mặt phẳng trung
trực của AB có dạng x + ay + bz + c =0.
Khi đó a + b + c bằng
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho mặt cầu ( S ) : x - 1 2 + y + 2 2 + z - 3 2 = 27 . Gọi α là mặt phẳng đi qua hai điểm A(0;0;-4) và B(2;0;0) cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là (C) có thể tích lớn nhất. Biết mặt phẳng α có phương trình dạng ax+by-z+c=0, khi đó a-b+c bằng:
A. -4.
B. 8.
C. 0.
D. 2.
Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+ (y+2)²+ (z-3)²=27. Gọi (α) là mặt phẳng đi qua hai điểm A (0; 0; -4), B (2; 0; 0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón đỉnh là tâm của (S) và đáy là là đường tròn (C) có thể tích lớn nhất. Biết rằng (α): ax+by-z+c=0, khi đó a-b+c bằng:
A. -4.
B. 8.
C. 0.
D. 2.
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2 x + y - 2 z - 2 = 0 đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng ( α ) , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 3
B. 7 2
C. 21 2
D. 3 2
Trong không gian Oxyz, cho tam giác ABC vuông tại C, A B C ^ = 60 o , A B = 3 2 Đường thẳng AB có phương trình x - 3 1 = y - 4 1 = z + 8 - 4 đường thẳng AC nằm trên mặt phẳng α : x+z-1=0 Biết B là điểm có hoành độ dương, gọi (a;b;c) là tọa độ của điểm C, giá trị của a+b+c bằng
A. 3
B. 2
C. 4
D. 7
Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23) và mặt cầu (S) có phương trình (S): (x - 5)2 + ( y + 3 )2 + (z + 2)2 = 72. Mặt phẳng (P): x + by + cz + d = 0 đi qua điểm A và tiếp xúc với mặt cầu (S) sao cho khoảng cách từ B đến mặt phẳng (P) lớn nhất. Giá trị của b + c + d khi đó là:
A. b + c + d = 2
B. b + c + d = 4
C. b + c + d = 3
D. b + c + d = 1
Trong không gian Oxyz, cho mặt phẳng (α): 2x+y-2z-2=0, đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A ( 1 2 ; 1 ; 1 ) . Gọi Δ là đường thẳng nằm trong mặt phẳng (α), song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:
A. 7/2
B. 21 / 2
C. 7/3
D. 3/2
Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0
Tìm điểm M' là ảnh của M(4; 2; 1) qua phép đối xứng qua mặt phẳng (α).
Trong không gian Oxyz cho điểm M(2;1;1) mặt phẳng α : x+y+z-4=0 và mặt cầu (S): x - 3 2 + ( y - 3 ) 2 + ( z - 4 ) 2 = 16 Phương trình đường thẳng α đi qua M và nằm trong α cắt mặt cầu (S) theo một đoạn thẳng có độ dài nhỏ nhất. Đường thẳng α đi qua điểm nào trong các điểm sau đây?
![]()
![]()
![]()
![]()