Question

Trong không gian Oxyz, cho điểm M(1;2;3). Biết rằng có tất cả n mặt phẳng dạng P i : x + a i y + b i z + c i = 0 i = 1 , 2 . . . n  đi qua M và cắt các trục tọa độ x'Ox, y'Oy, z'Oz lần lượt tại các điểm A, B, C khác gốc tọa độ O sao cho O.ABC là hình chóp đều. Giá trị của a 1 + a 2 + . . . + a n  bằng

A. 1

B. 3

C. -3

D. -1

Answer 1

 

Gọi A(a;0;0), B(0;b;0), C(0;0;c) có  và 

Vì O.ABC là hình chóp đều nên

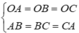
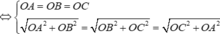
⇔ O A = O B = O C > 0

Do đó với  O A = O B = O C ⇔ a = b = c

Vậy ta có hệ điều kiện: 

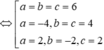
Vậy ta có ba mặt phẳng thoả mãn là

x+y=z-6=0; x-y-z+4=0; x-y+z-2=0

Vì vậy 

Chọn đáp án D.