Đáp án A.
Phương pháp:
+) Cho hai điểm ![]()
Khi đó ta có: ![]()
Cách giải:
Ta có:
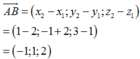
Đáp án A.
Phương pháp:
+) Cho hai điểm ![]()
Khi đó ta có: ![]()
Cách giải:
Ta có:
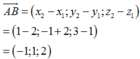
Trong không gian tọa độ Oxyz, cho điểm A(2;-1;3), B(4;0;1) và C(-10;5;3). Vecto nào dưới đây là véc tơ pháp tuyến của mặt phẳng (ABC) ?
A. (1;8;2)
B. (1;2;0)
C. (1;2;2)
D. (1;-2;2)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-2;-1;3) và B(0;3;1).Tọa độ trung điểm của đoạn thẳng AB là:
A. (-1;1;2)
B. (2;4;-2)
C. (-2;-4;2)
D. (-2;2;4)
Trong không gian Oxyz, cho A B ¯ = ( 1 ; - 2 ; 1 ) và điểm A(1;-2;4). Khi đó tọa độ của điểm B là
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho hai điểm A ( 1 ; 3 ; - 1 ) , B ( 2 ; - 1 ; 1 ) . Gọi M là điểm thỏa mãn B là trung điểm của đoạn thẳng AM tọa độ điểm M là
![]()
![]()

![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A, B với O A → = ( 2 ; - 1 ; 3 ) , O B → = = ( 5 ; 2 ; - 1 ) . Tìm tọa độ của vectơ A B → .
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A ( 1 ; - 1 ; 2 ) và B ( 2 ; 1 ; - 4 ) . Véctơ A B → có tọa độ là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm là A(1;3;-1), B(3;-1;5). Tìm tọa độ của điểm M thỏa mãn hệ thức M A → = 3 M B →
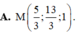
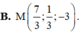
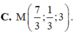
![]()
Trong không gian Oxyz, cho hai điểm A(2;-1;3), B(3;2;-4). Vectơ A B → có tọa độ là
A. (1;-3;7)
B. (1;3;-7)
C. (-1;3;-7)
D. (-1;-3;-7)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;1;0), B (0;1;2) . Vecto nào dưới đây là 1 vecto chỉ phương của đường thẳng AB?
A. a ⇀ (-1;0;-2)
B. b ⇀ (-1;0;-2)
C. c ⇀ (1;2;2)
D. d ⇀ (-1;1;2)