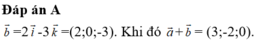Các câu hỏi tương tự
Trong không gian với hệ trục Oxyz, cho tam giác ABC với A(2;0;-3); B(-1;-2;4); C(2;-1;2). Biết điểm E(a,b,c) là điểm để biểu thức
P
E
A
→
+
E
B
→
+
E
C
→...
Đọc tiếp
Trong không gian với hệ trục Oxyz, cho tam giác ABC với A(2;0;-3); B(-1;-2;4); C(2;-1;2). Biết điểm E(a,b,c) là điểm để biểu thức P = E A → + E B → + E C → đạt giá trị nhỏ nhất. Tính T=a+b+c
A. T=3
B. T=1
C. T=0
D. T=-1
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(1;0;1),B(3;-2;0),C(1;2;-2). Gọi (P) là mặt phẳng đi qua A sao cho tổng khoảng cách từ B và C đến (P) lớn nhất biết rằng (P) không cắt đoạn BC. Khi đó vectơ pháp tuyến của mặt phẳng (P) là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(1;0;1),B(3;-2;0),C(1;2;-2). Gọi (P) là mặt phẳng đi qua A sao cho tổng khoảng cách từ B và C đến (P) lớn nhất biết rằng (P) không cắt đoạn BC. Khi đó vectơ pháp tuyến của mặt phẳng (P) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho
a
→
(
3
;
-
2
;
-
1
)
,
b
→
(
-
2
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho a → = ( 3 ; - 2 ; - 1 ) , b → = ( - 2 ; 0 ; - 1 ) . Độ dài a → + b → là:
A. 2
B. 3
C. 1
D. 2
Trong không gian Oxyz, cho
O
A
→
i
→
-
2
j
→
+
3
k
→
, điểm B(3;-4;1), C(2;0;-1) và điểm D(a;b;c) sao cho B là trọng tâm tam giác ABD. Khi đó Pa+b+c bằng A. 1 B. -3 C. -1 D. 3
Đọc tiếp
Trong không gian Oxyz, cho O A → = i → - 2 j → + 3 k → , điểm B(3;-4;1), C(2;0;-1) và điểm D(a;b;c) sao cho B là trọng tâm tam giác ABD. Khi đó P=a+b+c bằng
A. 1
B. -3
C. -1
D. 3
Trong không gian Oxyz, cho tám điểm A (-2;-2;0), B (3;-2;0), C (3;3;0), D (-2;3;0), M(-2;-2;5), N(3;3;5), P(3;-2;5), Q(-2;3;5) Hình đa diện tạo bởi tám điểm đã cho có bao nhiêu mặt đối xứng? A. 3 B. 9 C. 8 D. 6
Đọc tiếp
Trong không gian Oxyz, cho tám điểm A (-2;-2;0), B (3;-2;0), C (3;3;0), D (-2;3;0), M(-2;-2;5), N(3;3;5), P(3;-2;5), Q(-2;3;5) Hình đa diện tạo bởi tám điểm đã cho có bao nhiêu mặt đối xứng?
A. 3
B. 9
C. 8
D. 6
Trong không gian Oxyz, cho tám điểm A(-2;-2;0), B(3;-2;0), C(3;3;0), D(-2;3;0), M(-2;-2;5), N(3;3;5), P(3;-2;5), Q(-2;3;5). Hình đa diện tạo bởi tám điểm đã cho có bao nhiêu mặt đối xứng? A. 3. B. 9. C. 8. D. 6.
Đọc tiếp
Trong không gian Oxyz, cho tám điểm A(-2;-2;0), B(3;-2;0), C(3;3;0), D(-2;3;0), M(-2;-2;5), N(3;3;5), P(3;-2;5), Q(-2;3;5). Hình đa diện tạo bởi tám điểm đã cho có bao nhiêu mặt đối xứng?
A. 3.
B. 9.
C. 8.
D. 6.
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;0), B(0;2;0), C(0;0;3), D(2;-2;0). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D ? A. 7 B. 5 C. 6 D. 10
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;0), B(0;2;0), C(0;0;3), D(2;-2;0). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D ?
A. 7
B. 5
C. 6
D. 10
Trong không gian Oxyz, cho hai điểm A(1;-1;2),B(3;-4;-2)và đường thẳng
d
:
x
2
+
4
t
y
-
6
t...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;-1;2),B(3;-4;-2)và đường thẳng
d : x = 2 + 4 t y = - 6 t z = - 1 - 8 t . Điểm I(a,b,c) thuộc d là điểm thỏa mãn IA + IB đạt giá trị nhỏ nhất. Khi đó T = a + b + c bằng
A. 23 58
B. - 43 58
C. 65 29
D. - 21 58
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)CH 3. Trong không gian Oxyz cho 2 vectơ a (1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8CH 4.Trong không...
Đọc tiếp
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)
CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)
CH 3. Trong không gian Oxyz cho 2 vectơ a =(1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8
CH 4.Trong không gian Oxyz cho 2 vecto a= (3; 1; 2) và b= (2; 0; -1); khi đó vectơ 2a-b có độ dài bằng : А. 3/5 В. 29 С. M D. S/5
CH 5. Cho hình bình hành ABCD với A (-1;0;2), B(3;4;0) D (5;2;6). Tìm khẳng định sai. A. Tâm của hình bình hành có tọa độ là (4;3;3) B. Vecto AB có tọa độ là (4;-4;-2) C. Tọa độ của điểm C là (9;6;4) D. Trọng tâm tam giác ABD có tọa độ là (3;2;2)
Trong không gian Oxyz, cho hai điểm A(1;2;−3) và B(3; −2; −1). Tọa độ trung điểm đoạn thẳng AB là điểm
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;2;−3) và B(3; −2; −1). Tọa độ trung điểm đoạn thẳng AB là điểm
![]()
![]()
![]()
![]()