Các câu hỏi tương tự
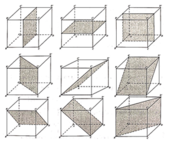
Trong không gian Oxyz, cho tám điểm A (-2;-2;0), B (3;-2;0), C (3;3;0), D (-2;3;0), M(-2;-2;5), N(3;3;5), P(3;-2;5), Q(-2;3;5) Hình đa diện tạo bởi tám điểm đã cho có bao nhiêu mặt đối xứng? A. 3 B. 9 C. 8 D. 6
Đọc tiếp
Trong không gian Oxyz, cho tám điểm A (-2;-2;0), B (3;-2;0), C (3;3;0), D (-2;3;0), M(-2;-2;5), N(3;3;5), P(3;-2;5), Q(-2;3;5) Hình đa diện tạo bởi tám điểm đã cho có bao nhiêu mặt đối xứng?
A. 3
B. 9
C. 8
D. 6
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;0), B(0;2;0), C(0;0;3), D(2;-2;0). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D ? A. 7 B. 5 C. 6 D. 10
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;0), B(0;2;0), C(0;0;3), D(2;-2;0). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D ?
A. 7
B. 5
C. 6
D. 10
Trong không gian Oxyz, cho A(0;0;-3), B(2;0;-1) và mp (P): 3x-8y+7z-10. Có bao nhiêu điểm C trên mặt phẳng (P) sao cho ABC đều. A. vố số B. 1 C. 3 D. 2
Đọc tiếp
Trong không gian Oxyz, cho A(0;0;-3), B(2;0;-1) và mp (P): 3x-8y+7z-1=0. Có bao nhiêu điểm C trên mặt phẳng (P) sao cho ABC đều.
A. vố số
B. 1
C. 3
D. 2
Trong không gian Oxyz, có hai mặt phẳng (P), (Q) cách đều hai điểm A(3;-2;0), B(1;0;2) và chứa đường thẳng
d
:
x
-
1
3
y
-
1
1
z
+
1
-
2
. Giá trị sin góc tạo bởi hai mặt phẳng...
Đọc tiếp
Trong không gian Oxyz, có hai mặt phẳng (P), (Q) cách đều hai điểm A(3;-2;0), B(1;0;2) và chứa đường thẳng d : x - 1 3 = y - 1 1 = z + 1 - 2 . Giá trị sin góc tạo bởi hai mặt phẳng (P) và (Q) bằng
A. 2 3 .
B. 3 2 .
C. 7 3 .
D. 1 3 .
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;-2;0), B (-3;2;-4) và mặt phẳng (P): x + 2y + z - 3 0. Gọi M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho tam giác MAB cân tại M và có diện tích nhỏ nhất. Tính giá trị
T
a
2
+
b
+
c
. A. T 1 B. T 2 C. T 0 D. T 3
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A (1;-2;0), B (-3;2;-4) và mặt phẳng (P): x + 2y + z - 3 = 0.
Gọi M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho tam giác
MAB cân tại M và có diện tích nhỏ nhất. Tính giá trị T = a 2 + b + c .
A. T = 1
B. T = 2
C. T = 0
D. T = 3
Trong không gian Oxyz, cho
O
A
→
i
→
-
2
j
→
+
3
k
→
, điểm B(3;-4;1), C(2;0;-1) và điểm D(a;b;c) sao cho B là trọng tâm tam giác ABD. Khi đó Pa+b+c bằng A. 1 B. -3 C. -1 D. 3
Đọc tiếp
Trong không gian Oxyz, cho O A → = i → - 2 j → + 3 k → , điểm B(3;-4;1), C(2;0;-1) và điểm D(a;b;c) sao cho B là trọng tâm tam giác ABD. Khi đó P=a+b+c bằng
A. 1
B. -3
C. -1
D. 3
Trong không gian tọa độ Oxyz, cho bốn điểm
A
(
1
;
-
2
;
0
)
,
B
(
3
;
3
;
2
)
,
C
(
-
1
;
2
;
2
)
,
D
(
3
;
3
;
1
)
.
Độ dài đường cao của tứ diện ABCD hạ...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho bốn điểm A ( 1 ; - 2 ; 0 ) , B ( 3 ; 3 ; 2 ) , C ( - 1 ; 2 ; 2 ) , D ( 3 ; 3 ; 1 ) . Độ dài đường cao của tứ diện ABCD hạ từ đỉnh D xuống mặt phẳng (ABC) là
A. 9 7 2
B. 9 7
C. 9 2
D. 9 14
Trong không gian với hệ tọa độ Oxya, cho tứ diện ABCD có A(-1;1;6), B(-3;-2;-4), C(1;2;-1), D(2;-2;0). Điểm M(a,b,c) thuộc đường thẳng CD sao cho tam giác ABM có chu vi nhỏ nhất. Tính a+b+c. A.1. B.2. C.3. D.0.
Đọc tiếp
Trong không gian với hệ tọa độ Oxya, cho tứ diện ABCD có A(-1;1;6), B(-3;-2;-4), C(1;2;-1), D(2;-2;0). Điểm M(a,b,c) thuộc đường thẳng CD sao cho tam giác ABM có chu vi nhỏ nhất. Tính a+b+c.
A.1.
B.2.
C.3.
D.0.
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;-1), C(6;1;0). Hình thang có diện tích bằng 6√2. Giả sử đỉnh D(a;b;c), tìm mệnh đề đúng? A. a+b+c6 B. a+b+c5 C. a+b+c8 D. a+b+c7
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;-1), C(6;1;0). Hình thang có diện tích bằng 6√2. Giả sử đỉnh D(a;b;c), tìm mệnh đề đúng?
A. a+b+c=6
B. a+b+c=5
C. a+b+c=8
D. a+b+c=7