Chọn B

Gọi A là một điểm thuộc d => tọa độ của A thỏa mãn HPT

Chọn B

Gọi A là một điểm thuộc d => tọa độ của A thỏa mãn HPT

Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng α : 2 x + 4 y − 5 z + 2 = 0 , β : x + 2 y − 2 z + 1 = 0 và γ : 4 x − m y + z + n = 0 . Để ba mặt phẳng đó có chung giao tuyến thì tổng m+n bằng
A. -4
B. 8
C.-8
D. 4
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - y - z + 1 = 0 và (Q): 2x + 3y - z = 0. Viết phương trình chính tắc của đường thẳng giao tuyến D của hai mặt phẳng (P) và (Q). Chọn khẳng định sai

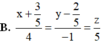
![]()
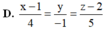
Trong không gian Oxyz, cho mặt phẳng α : 2 x + 3 y - 2 z + 12 = 0 . Gọi A, B, C lần lượt là giao điểm của α với 3 trục tọa độ, đường thẳng d đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với α có phương trình là
![]()
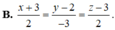
![]()
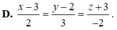
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): x + y - 5z + 4 = 0 và đường thẳng d : x + 1 2 = y + 1 1 = z + 5 6 . Hình chiếu vuông góc của đường thẳng d trên mặt phẳng (P) có phương trình là
A. x = - 2 + 3 t y = - 2 + t z = - t
B. x = - 2 + t y = 2 + 2 t z = t
C. x = 1 + 3 t y = 2 t z = 1 + t
D. x = 3 + t y = 2 z = 1 + t
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng (P): 3x -2y+2z-5=0 và (Q): 4x+5y-z+1=0 Các điểm A, B phân biệt thuộc giao tuyến của hai mặt phẳng (P) và (Q) cùng phương với vectơ nào sau đây?
A. w → = ( 3 ; - 2 ; 2 )
B. v → = ( - 8 ; 11 ; - 23 )
C. a → = ( 4 ; 5 ; - 1 )
D. u → = ( 8 ; - 11 ; - 23 )
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x 2 = y - 3 1 = z - 2 1 và hai mặt phẳng
(P): x-2y+2z=0. (Q): x-2y+3z-5=0. Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiếp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S).
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-1;-2;2), B((-3;-2;0) và mặt phẳng (P):x+3y-z+2=0. Vectơ chỉ phương của đường thẳng d là giao tuyến của mặt phẳng (P) và mặt phẳng trung trực của đoạn AB có tọa độ là:
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, phương trình của mặt phẳng (P) đi qua điểm B(2;1;-3), đồng thời vuông góc với hai mặt phẳng (Q): x+y+3z=0, (R): 2x-y+z=0 là
![]()
![]()
![]()
![]()
Phương trình mặt phẳng qua giao tuyến của hai mặt phẳng (P)x-3y+2z-1=0 và (Q)2x+y-3z+1=0 và song song với trục Ox là