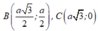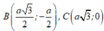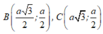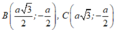\(B\in Ox\Rightarrow B\left(x;0\right)\)
\(AB\perp BC\) (\(ABCD\) là hình vuông)
mà \(\overrightarrow{BC}\) cùng hướng \(\overrightarrow{i}\) là vec tơ đơn vị trên trục \(Ox\)
\(\Rightarrow AB//Oy\)
\(\Rightarrow B\left(1;0\right)\) (cùng hoành độ với \(A\left(1;3\right)\))
Gọi \(C\left(x;0\right)\in Ox\left(B\in Ox;AB\perp BC\right)\)
\(AB=BC\) \(\)(\(ABCD\) là hình vuông)
\(\Leftrightarrow\sqrt{\left(1-1\right)^2+\left(0-3\right)^2}=\left|x-1\right|\)
\(\Leftrightarrow\left|x-1\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=3\\x-1=-3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
\(\Leftrightarrow C\left(4;0\right)\) hay \(C\left(-2;0\right)\)
Vì \(\overrightarrow{BC}=\left(x-1;0\right)\) cùng hướng \(\overrightarrow{i}=\left(1;0\right)\)
\(\Rightarrow\dfrac{x-1}{1}>0\)
\(\Rightarrow x>1\)
Vậy \(C\left(4;0\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(3;-3\right)\)