Trong hệ trục Oxy, cho 3 điểm A(2;2) , B(1;-1) , C(-1;-7)
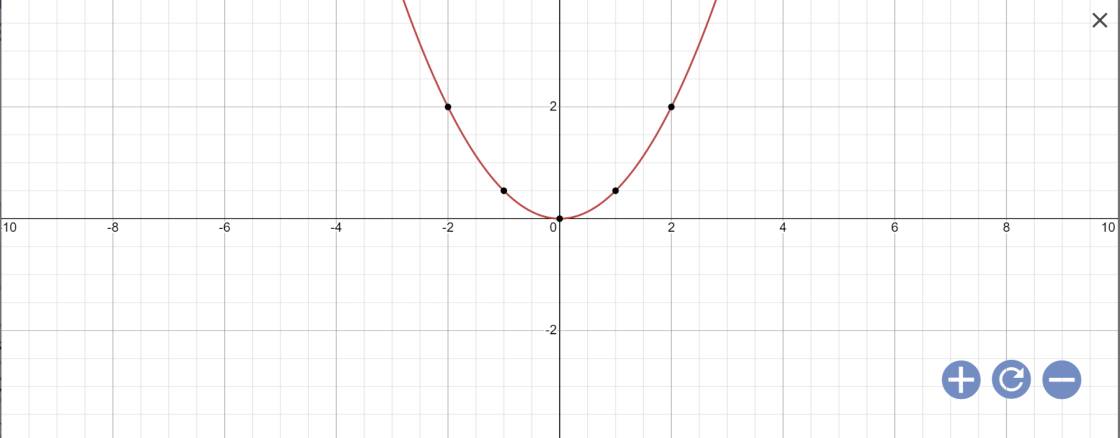
a) Tìm hệ số a của hàm số y = ax² biết đồ thị của nó đi qua điểm A. Vẽ đồ thị (P) ứng với a tìm được.
b) 3 điểm A, B, C có thẳng hàng không?
c) Gọi M là 1 điểm tùy ý thuộc (P), I là trung điểm OM. Chứng minh khi điểm M di chuyển trên (P) thì I di chuyển trên (P'): y = x².
a: Thay x=2 và y=2 vào (P): ta được:
\(a\cdot2^2=2\)
=>4a=2
=>\(a=\dfrac{1}{2}\)
Vậy: (P): \(y=\dfrac{1}{2}x^2\)
b: A(2;2); B(1;-1); C(-1;-7)
\(\overrightarrow{AB}=\left(-1;-3\right);\overrightarrow{AC}=\left(-3;-9\right)\)
Vì \(\dfrac{-1}{-3}=\dfrac{-3}{-9}\left(=\dfrac{1}{3}\right)\)
nên A,B,C thẳng hàng













