Các câu hỏi tương tự
Cho hàm số y f(x) ln(x+1). Mệnh đề nào sau đây là đúng? A. Đồ thị của hàm số y f(x) cắt trục hoành tại 1 điểm B. Phương trình f(x) 0 có nghiệm x 1 C. Đồ thị của hàm số y f(x) không cắt trục hoành D. Phương trình f(x) 0 có nghiệm x -1
Đọc tiếp
Cho hàm số y = f(x) = ln(x+1). Mệnh đề nào sau đây là đúng?
A. Đồ thị của hàm số y = f'(x) cắt trục hoành tại 1 điểm
B. Phương trình f'(x) = 0 có nghiệm x = 1
C. Đồ thị của hàm số y = f'(x) không cắt trục hoành
D. Phương trình f'(x) = 0 có nghiệm x = -1
Cho các mệnh đề sau đây:(1) Hàm số
f
(
x
)
log
2
2
x
-
log
2
x
4
+
4
có tập xác định
D
[
0
;
+
∞
)
(2) Hàm số
y
log
a
x
có tiệm cận ngang(3) Hàm số
y
log
a
x
;
...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Cho hàm số y f(x) xác định trên
D
−
1
;
+
∞
1
.
Dưới đây là một phần đồ thị của y f(x)Hỏi trong các mệnh đề sau, có bao nhiêu mệnh đề đúng: (I) Số điểm cực đại của hàm số trên tập xác định là 1. (II) Hàm số có cực tiểu là -2 tại x 1 (III) Hàm số đạt cực đại tại x 2 (IV) Hàm số đạt cực đại tại x -1 A. 0 B. 1 C. 2 D...
Đọc tiếp
Cho hàm số y = f(x) xác định trên D = − 1 ; + ∞ \ 1 . Dưới đây là một phần đồ thị của y = f(x)
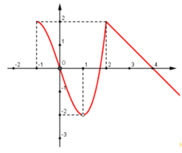
Hỏi trong các mệnh đề sau, có bao nhiêu mệnh đề đúng:
(I) Số điểm cực đại của hàm số trên tập xác định là 1.
(II) Hàm số có cực tiểu là -2 tại x = 1
(III) Hàm số đạt cực đại tại x = 2
(IV) Hàm số đạt cực đại tại x = -1
A. 0
B. 1
C. 2
D. 3
Cho hàm số
f
x
log
2
x
,
g
x
2
x
. Xét các mệnh đề sau: (I) Đồ thị hai hàm số đối xứng nhau qua đường thẳng y x (II) Tập xác định của hai hàm số trên là
ℝ
(III) Đồ thị hai hàm số cắt nhau tại đúng 1 điểm. (IV) Hai hàm số đều đồng biến trên tập xác định của nó. Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A....
Đọc tiếp
Cho hàm số f x = log 2 x , g x = 2 x . Xét các mệnh đề sau:
(I) Đồ thị hai hàm số đối xứng nhau qua đường thẳng y = x
(II) Tập xác định của hai hàm số trên là ℝ
(III) Đồ thị hai hàm số cắt nhau tại đúng 1 điểm.
(IV) Hai hàm số đều đồng biến trên tập xác định của nó.
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 2
B. 3
C. 1
D. 4
Cho hàm số yf(x) xác định, liên tục trên tập R{1} và có bảng biến thiênSố mệnh đề đúng trong các mệnh đề sau là? 1. Đường thẳng y2 là đường tiệm cận ngang của đồ thị hàm số. 2. Đường thẳng x1 là đường tiệm cận đứng của đồ thị hàm số. 3. Hàm số đồng biến trên các khoảng
-
∞
;
1
và
1
;
+
∞
A. 0. B....
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên tập R\{1} và có bảng biến thiên
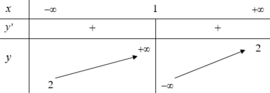
Số mệnh đề đúng trong các mệnh đề sau là?
1. Đường thẳng y=2 là đường tiệm cận ngang của đồ thị hàm số.
2. Đường thẳng x=1 là đường tiệm cận đứng của đồ thị hàm số.
3. Hàm số đồng biến trên các khoảng - ∞ ; 1 và 1 ; + ∞
A. 0.
B. 1
C. 2.
D. 3
Cho các mệnh đề sau:(I). Nếu
a
b
c
t
h
ì
2
ln
a
ln
b
+
ln
c
(II). Cho số thực 0 a ≠ 1. Khi đó
a
-
1
log
a
x
≥
0...
Đọc tiếp
Cho các mệnh đề sau:
(I). Nếu a = b c t h ì 2 ln a = ln b + ln c
(II). Cho số thực 0 < a ≠ 1. Khi đó a - 1 log a x ≥ 0 ⇔ x ≥ 1
(III). Cho các số thực 0 < a ≠ 1 , b > 0 , c > 0 . Khi đó b log a c ≥ 0 ⇔ x ≥ 1
(IV). l i m x → + ∞ 1 2 x = - ∞ .
Số mệnh đề đúng trong các mệnh đề trên là
A. 3
B. 4
C. 2
D. 1
Cho các mệnh đề sau đây:(1) Ta có biểu thức sau
log
3
x
+
5
+
log
9
x
-
2
2
-
log
3
x
-
1
log
3
x
+...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Ta có biểu thức sau log 3 x + 5 + log 9 x - 2 2 - log 3 x - 1 = log 3 x + 5 x - 2 x - 1 2
(2) Hàm số log 3 x - 3 2 có tập xác định là D = R.
(3) Hàm số y = log a x có đạo hàm ở tại mọi điểm x > 0 .
(4) Tập xác định D của hàm số y = 2 x - 1 + ln 1 - x 2 là: D = 1 2 ; 1 .
(5) Đạo hàm của hàm số y = 2 x - 1 + ln 1 - x 2 là 1 2 x - 1 - 2 x 1 - x 2 .
Hỏi có bao nhiêu mệnh đề đúng:
A. 2
B. 4
C. 3
D. 5
Cho hàm số
y
f
(
x
)
liên tục trên
ℝ
và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau(1) Hàm số
y
f
(
x
)
đạt cực đại tại
x
0
0
(2) Hàm số
y
f
(
x
)
có ba cực trị.(3) Phương trình
y
f
(
x
)
có đúng ba nghiệm phân biệt(4) Hàm...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên ℝ và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau
(1) Hàm số y = f ( x ) đạt cực đại tại x 0 = 0
(2) Hàm số y = f ( x ) có ba cực trị.
(3) Phương trình y = f ( x ) có đúng ba nghiệm phân biệt
(4) Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Hỏi trong 4 mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 1
B. 3
C. 4
D. 2
Cho hai hàm số
f
(
x
)
log
2
x
,
g
(
x
)
2
x
. Xét các mệnh đề sau: I. Đồ thị hàm số đối xứng với nhau qua đường thẳng yx II. Tập xác định của hai hàm số trên là R III. Đồ thị hai hàm số cắt nhau tại đúng 1 điểmIV. Hai hàm số đều đồng biến trên tập xác định của nóCó bao nhiêu mệnh đề đúng trong các mệnh đề trên A...
Đọc tiếp
Cho hai hàm số f ( x ) = log 2 x , g ( x ) = 2 x . Xét các mệnh đề sau:
I. Đồ thị hàm số đối xứng với nhau qua đường thẳng y=x
II. Tập xác định của hai hàm số trên là R
III. Đồ thị hai hàm số cắt nhau tại đúng 1 điểm
IV. Hai hàm số đều đồng biến trên tập xác định của nó
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên
A. 2
B. 3
C. 1
D. 4
Cho hai hàm số
y
e
x
và
y
ln
x
. Xét các mệnh đề sau (I) Đồ thị hai hàm số đối xứng qua đường thẳng yx(II) Tập xác định của hai hàm số trên là R (III) Đồ thị hai hàm số cắt nhau tại đúng một điểm. (IV) Hai hàm số đều đồng biến trên tập xác định của nó.Có bao nhiêu mệnh đề sai trong các mệnh đề trên? A. 2 B. 3 C. 1 D. 4
Đọc tiếp
Cho hai hàm số y = e x và y = ln x . Xét các mệnh đề sau
(I) Đồ thị hai hàm số đối xứng qua đường thẳng y=x
(II) Tập xác định của hai hàm số trên là R
(III) Đồ thị hai hàm số cắt nhau tại đúng một điểm.
(IV) Hai hàm số đều đồng biến trên tập xác định của nó.
Có bao nhiêu mệnh đề sai trong các mệnh đề trên?
A. 2
B. 3
C. 1
D. 4




