, phần thực của 
không lớn hơn môđun của 
.
, phần ảo của 
không lớn hơn môđun của 
.
, môđun của 
và môđun của 
luôn bằng nhau.
Các câu hỏi tương tự
Cho số phức z có phần thực là 2 và phần ảo là -3 . Môđun của số phức 3+izlà:
Đọc tiếp
Cho số phức z có phần thực là 2 và phần ảo là -3 . Môđun của số phức 3+izlà:
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn
z
+
1
+
i
z
¯
+
i
. Tổng phần thực và phần ảo của số phức z bằng
Đọc tiếp
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn z + 1 + i = z ¯ + i . Tổng phần thực và phần ảo của số phức z bằng
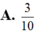
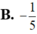
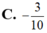
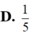
Trong các số phức z thỏa mãn
z
2
+
1
2
z
, gọi
z
1
và
z
2
lần lượt là các số phức có môđun lớn nhất và nhỏ nhất. Khi đó môđun lớn nhất của số phức
w
...
Đọc tiếp
Trong các số phức z thỏa mãn z 2 + 1 = 2 z , gọi z 1 và z 2 lần lượt là các số phức có môđun lớn nhất và nhỏ nhất. Khi đó môđun lớn nhất của số phức w = z 1 + z 2 là:
Trong các số phức z thỏa mãn
z
2
+
1
2
z
, gọi
z
1
và
z
2
lần lượt là các số phức có môđun lớn nhất và nhỏ...
Đọc tiếp
Trong các số phức z thỏa mãn z 2 + 1 = 2 z , gọi z 1 và z 2 lần lượt là các số phức có môđun lớn nhất và nhỏ nhất.
Khi đó môđun lớn nhất của số phức w = z 1 + z 2 là:
A. w = 2 2
B. w = 2
C. w = 2
D. w = 1 + 2
Trong các số phức z thỏa mãn điều kiện
z
+
2
-
3
i
z
+
1
-
2
i
, hãy tìm phần ảo của số phức có môđun nhỏ nhất? A.
10
13
B.
2
5
C...
Đọc tiếp
Trong các số phức z thỏa mãn điều kiện z + 2 - 3 i = z + 1 - 2 i , hãy tìm phần ảo của số phức có môđun nhỏ nhất?
A. 10 13
B. 2 5
C. -2
D. - 2 13
Trong các số phức z thỏa mãn điều kiện
z
-
2
-
4
i
z
-
2
i
Số phức z có môđun nhỏ nhất có tổng phần thực và phần ảo là A. 0. B. 4. C. 3. D. 2.
Đọc tiếp
Trong các số phức z thỏa mãn điều kiện z - 2 - 4 i = z - 2 i Số phức z có môđun nhỏ nhất có tổng phần thực và phần ảo là
A. 0.
B. 4.
C. 3.
D. 2.
Cho số phức z có phần thực là số nguyên và z thỏa mãn
z
-
2
z
-
7
+
3
i
+
z
. Môđun của số phức
w
1
-
z
+
z
2
bằng A.
w
445
B.
w...
Đọc tiếp
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z = - 7 + 3 i + z . Môđun của số phức w = 1 - z + z 2 bằng
A. w = 445
B. w = 425
C. w = 37
D. w = 457
Với các số thực a, b biết phương trình
z
2
+
8
a
z
+
64
b
0
có nghiệm phức
z
0
8
+
16
i
Tính môđun của số phức
w
a
+
b
i
Đọc tiếp
Với các số thực a, b biết phương trình z 2 + 8 a z + 64 b = 0 có nghiệm phức z 0 = 8 + 16 i Tính môđun của số phức w = a + b i
Cho số phức z a + bi với
a
,
b
∈
ℝ
. Môđun của z tính bằng công thức nào sau đây?
Đọc tiếp
Cho số phức z = a + bi với a , b ∈ ℝ . Môđun của z tính bằng công thức nào sau đây?
Trong tập hợp các số phức z thỏa mãn:
z
+
2
-
i
z
+
1
-
i
2
Tìm môđun lớn nhất của số phức z +i A.
2
+
2
B.
3
+
2
C. ...
Đọc tiếp
Trong tập hợp các số phức z thỏa mãn: z + 2 - i z + 1 - i = 2 Tìm môđun lớn nhất của số phức z +i
A. 2 + 2
B. 3 + 2
C. 3 - 2
D. 2 - 2