Chọn A.
Đặt z = a + bi khi đó ![]()
Thay vào phương trình: ![]()
Suy ra 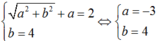
Chọn A.
Đặt z = a + bi khi đó ![]()
Thay vào phương trình: ![]()
Suy ra 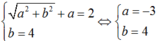
Tìm số phức Z, biết Z là nghiệm của phương trình: ( 2 i - 1 ) Z 2 - 2 i Z ¯ + ( 6 + 4 i ) = 0
A. Z = -i
B. Z = 1-i
C. Z = 1+i
D. Z = i
Biết các số phức z thỏa mãn |z-3|=|z+4i|. Tìm w m i n biết w = z + 4i -3
A. w m i n = 7 5
B. w m i n = 7 10
C. w m i n = 7 12
D. w m i n = 7
Giải các phương trình sau trên tập số phức:
(7 - 3i)z + (2 + 3i) = (5 - 4i)z
Biết rằng hai số phức z 1 , z 2 thỏa mãn | z 1 - 3 - 4 i | = 1 và | z 2 - 3 - 4 i | = 1 2 . Số phức z có phần thực là a và phần ảo là b thỏa mãn 3 a - 2 b = 12 . Giá trị nhỏ nhất của P = | z - z 1 | + | z - 2 z 2 | + 2 bằng:
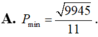
![]()
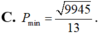
![]()
Biết số phức z=-3+4i là một nghiệm của phương trình z 2 - a z + b = 0 trong đó a, b là các số thực. Tính a-b
![]()
![]()
![]()
D.-19
Biết số phức z = -3 +4i là một nghiệm của phương trình z 2 + a z + b = 0 , trong đó a, b là các số thực. Tính a -b.
A. -31
B. -19
C. 1
D. -11
Phần thực của số z thỏa mãn phương trình: (5 - 4i) z = ( 3 + 2i)(4 - i) gần với giá trị nào nhất.
A. 1,21.
B. 1,22.
C. 1,23.
D. 1,24.
Trong các số phức z thỏa mãn z = z - 2 + 4 i , số phức có môđun nhỏ nhất là.
A. z =5
B. z = 5 2 i
C. z = 1 +2i
D. z = 3+i
Cho phức z thỏa z - z = - 2 - 4 i . Môđun của z là
A. 3.
B. 25.
C. 5.
D. 4.