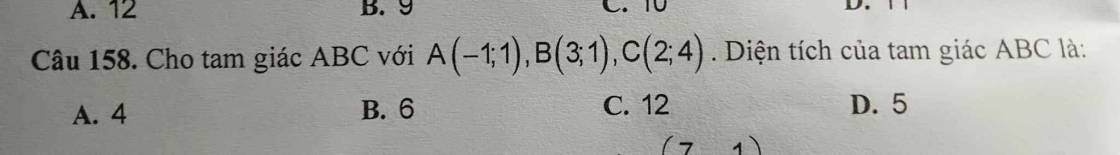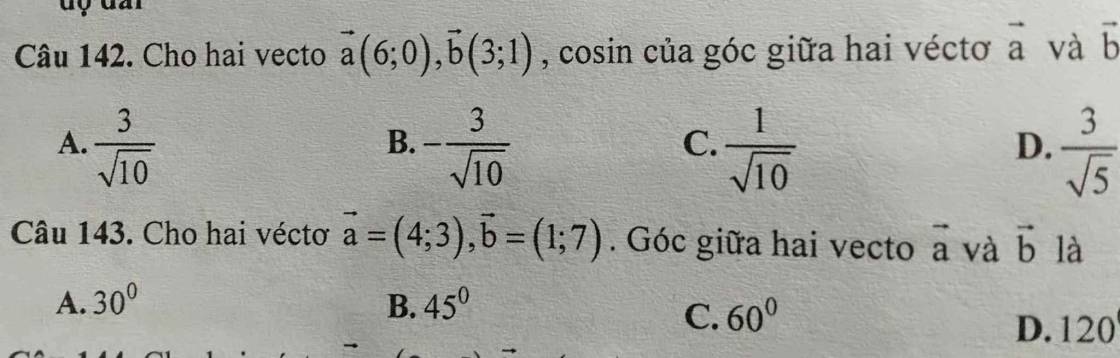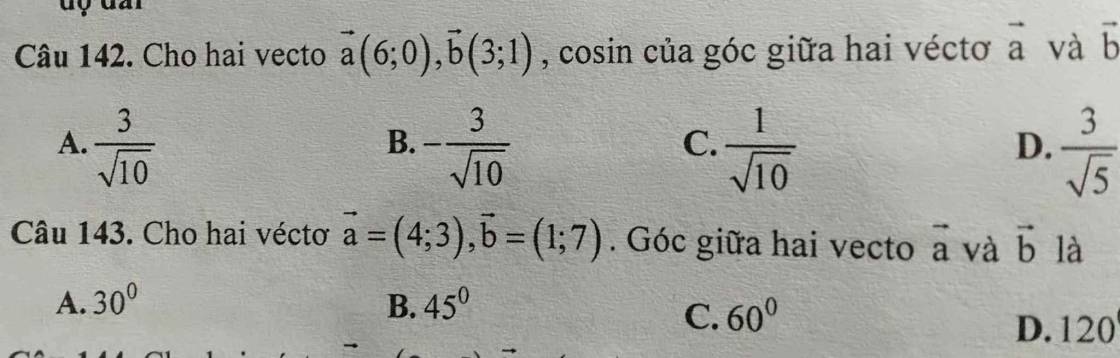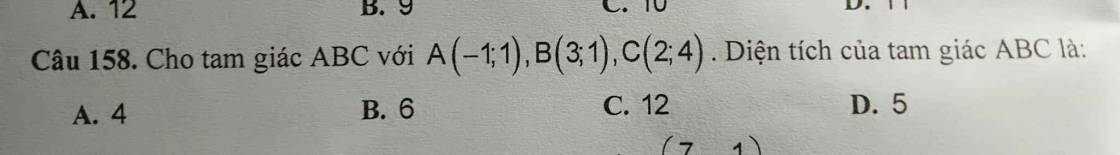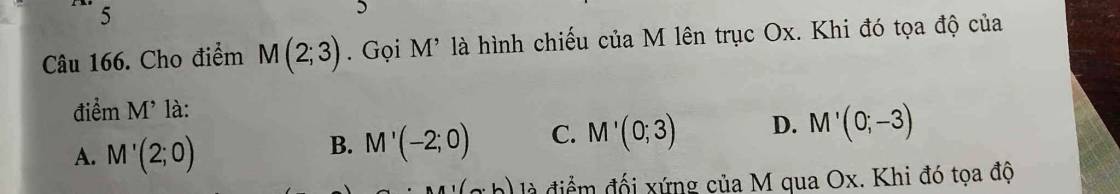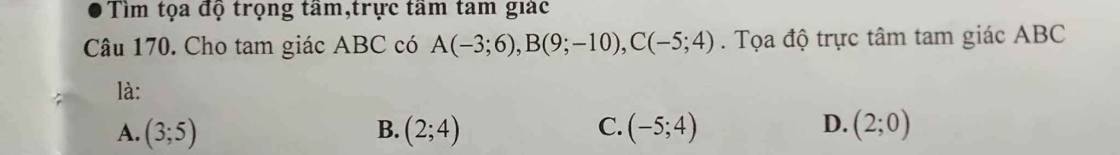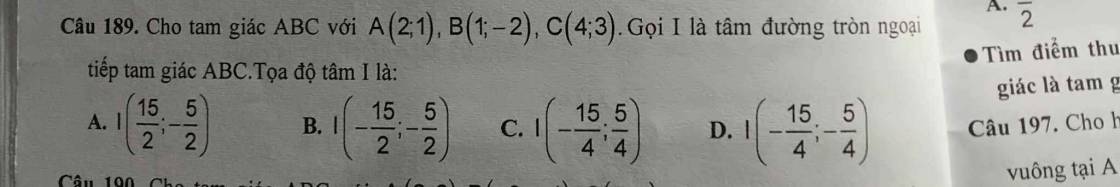Câu 158:
A(-1;1); B(3;1); C(2;4)
\(AB=\sqrt{\left(3+1\right)^2+\left(1-1\right)^2}=4\)
\(AC=\sqrt{\left(2+1\right)^2+\left(4-1\right)^2}=\sqrt{3^2+3^2}=3\sqrt{2}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(4-1\right)^2}=\sqrt{3^2+1^2}=\sqrt{10}\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{16+18-10}{2\cdot4\cdot3\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
=>\(sinBAC=\sqrt{1-cos^2BAC}=\dfrac{\sqrt{2}}{2}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\cdot4\cdot3\sqrt{2}=6\)
=>Chọn B
Câu 143:
\(\overrightarrow{a}=\left(4;3\right);\overrightarrow{b}=\left(1;7\right)\)
\(\overrightarrow{a}\cdot\overrightarrow{b}=4\cdot1+3\cdot7=25\)
\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|}=\dfrac{25}{\sqrt{\left(4^2+3^2\right)}\cdot\sqrt{1^2+7^2}}=\dfrac{25}{5\cdot5\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)=>\(\left(\overrightarrow{a};\overrightarrow{b}\right)=45^0\)
=>Chọn B
Câu 142:
\(\overrightarrow{a}=\left(6;0\right);\overrightarrow{b}=\left(3;1\right)\)
\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|}=\dfrac{6\cdot3+1\cdot0}{\sqrt{6^2+0^2}\cdot\sqrt{3^2+1^2}}=\dfrac{18}{6\cdot\sqrt{10}}=\dfrac{3}{\sqrt{10}}\)
=>Chọn A
Câu 131:
Đặt \(\overrightarrow{c}=x\cdot\overrightarrow{a}+y\cdot\overrightarrow{b}\)
=>\(\left\{{}\begin{matrix}2x+\left(-4\right)y=-6\\3x+3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6x-12y=-18\\12x+12y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}18x=-14\\x+y=\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{7}{9}\\y=\dfrac{1}{3}-x=\dfrac{1}{3}+\dfrac{7}{9}=\dfrac{10}{9}\end{matrix}\right.\)
=>Chọn A
giúp em với ạ , trình bày như tự luận 
