\(a,=\dfrac{1-2x+3+2y+2x-4}{6x^3y}=\dfrac{2y}{6x^3y}=\dfrac{1}{3x^2}\\ b,=\dfrac{4x-8+2x+4-5x+6}{\left(x+2\right)\left(x-2\right)}=\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x+2}\\ c,=\dfrac{x^2+2+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\\ d,=\dfrac{1}{\left(x+3\right)^2}-\dfrac{1}{\left(x-3\right)^2}+\dfrac{x}{\left(x-3\right)\left(x+3\right)}\\ =\dfrac{x^2-6x+9-x^2-6x-9+x^3-9x}{\left(x+3\right)^2\left(x-3\right)^2}=\dfrac{x^3-21x}{\left(x+3\right)^2\left(x-3\right)^2}\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
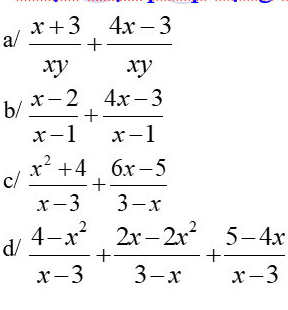 trình bày đầy đủ nha
trình bày đầy đủ nha
trình bày đầy đủ nha
Đọc tiếp
trình bày đầy đủ nha
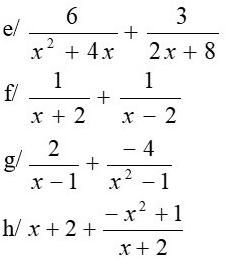 trình bày đầy đủ nha
trình bày đầy đủ nha
trình bày đầy đủ nha
Đọc tiếp
trình bày đầy đủ nha
 trình bày đầy đủ nha
trình bày đầy đủ nha
trình bày đầy đủ nha
Đọc tiếp
trình bày đầy đủ nha
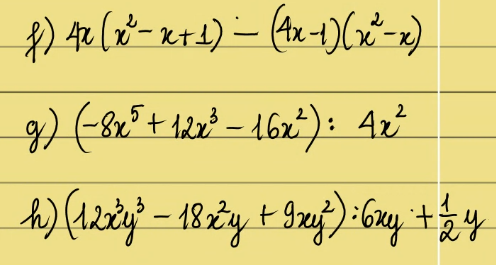 trình bày đầy đủ nha
trình bày đầy đủ nha
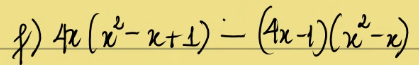 trình bày đầy đủ nha
trình bày đầy đủ nha
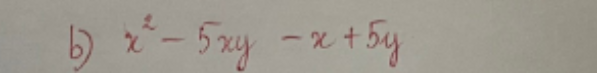 trình bày đầy đủ nha
trình bày đầy đủ nha

 trình bày đầy đủ nha
trình bày đầy đủ nha

