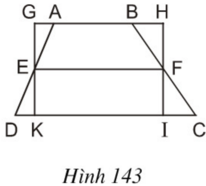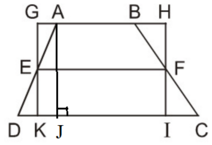
Ta có hình thang ABCD (AB // CD) với đường trung bình EF và hình chữ nhật GHIK như hình vẽ.
Dễ dàng chứng minh:
ΔAEG = ΔDEK, ΔBFH = ΔCFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên SABCD = SGHIK
Mà SGHIK = GH.GK= EF. AJ ( vì GH = EF, GK = AJ)
Nên SABCD = EF. AJ
Lại có:
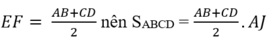
Vậy ta gặp lại công thức tính diện tích hình thang đã học nhưng bằng một phương pháp chứng minh khác.
Mặt khác, ta phát hiện công thức mới: Diện tích hình thang bằng tích của đường trung bình hình thang với đường cao.