Question

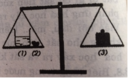
Trên hai đĩa cân để 2 cốc đựng 100 gam dung dịch axit clohiđric 7,3% (cốc 1) và 100 gam dung dịch axit sunfuric 9,8% (cốc 2) sao cho cân ở vị trí thăng bằng. - Thêm vào cốc thứ nhất 3 gam canxi cacbonat khuấy đều thấy thoát ra V lít khí CO2. - Thêm vào cốc thứ hai x gam nhôm, khuấy đều thấy thoát ra V lít khí hiđro. Biết các thể tích khí đều đo ở điều kiện tiêu chuẩn. a/ Viết phương trình hóa học của các phản ứng xảy ra, biết canxi cacbonat phản ứng với axit clohiđric tạo thành canxi clorua, khí cacbonic và nước. b/ Tính V. c/ Sau các thí nghiệm, thấy cân vẫn thăng bằng. Tìm các giá trị x và V. d/ Tính nồng độ phần trăm chất tan trong dung dịch của cốc 1 sau khi phản ứng kết thúc.

HELP Me Plssssssssss

Answer 1

\(a,m_{HCl}=\dfrac{100.7,3}{100}=7,3\left(g\right)\\ \rightarrow n_{HCl}=\dfrac{7,3}{36,5}=0,2\left(mol\right)\\ m_{H_2SO_4}=\dfrac{9,8.100}{100}=9,8\left(mol\right)\\ \rightarrow n_{H_2SO_4}=\dfrac{9,8}{98}=0,1\left(mol\right)\\ n_{CaCO_3}=\dfrac{3}{100}=0,03\left(mol\right)\\ n_{Al}=\dfrac{x}{27}\left(mol\right)\)

PTHH:

               \(CaCO_3+2HCl\rightarrow CaCl_2+CO_2\uparrow+H_2O\)

ban đầu     0,03        0,2

phản ứng  0,03        0,06

sau pư         0           0,14       0,03       0,03       0,03

                           \(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\) (*)

- TH₁: Al hết       \(\dfrac{x}{27}\)------------------------------------->\(\dfrac{x}{18}\)

- TH₂: Al dư                     0,1------------------------>0,1

\(b,V_{CO_2}=0,03.22,4=0,672\left(l\right)\)

\(c,m_{cốc\left(1\right)}=3+100-0,03.2=102,94\left(g\right)\)

TH₁: Al tan hết

\(m_{cốc\left(2\right)}=x+100-\dfrac{x}{18}.2=\dfrac{8x}{9}+100\left(g\right)\)

Do \(m_{cốc\left(1\right)}=m_{cốc\left(2\right)}\)

\(\rightarrow102,94=\dfrac{8x}{9}+100\\ \Leftrightarrow x=3,3075\left(g\right)\)

\(V_{H_2}=\dfrac{3,3075}{18}.22,4=4,116\left(l\right)\)

- TH₂: Al dư

\(m_{cốc\left(2\right)}=x+100-0,1.2=99,8+x\left(g\right)\)

\(\rightarrow102,94=99,8+x\\ \Leftrightarrow x=3,14\left(g\right)\)

\(V_{H_2}=0,1.22,4=2,24\left(l\right)\)

\(d,\left\{{}\begin{matrix}C\%_{CaCl_2}=\dfrac{0,03.111}{102,94}.100\%=3,23\%\\C\%_{HCl\left(dư\right)}=\dfrac{0,14.36,5}{102,94}.100\%=4,96\%\end{matrix}\right.\)

Answer 2

\(pthh:2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\\ 2HCl+CaCO_3\rightarrow CaCl_2+CO_2+H_2O\) 
\(m_{HCl}=\dfrac{100.7,3}{100}=7,3\left(g\right)\\ n_{HCl}=\dfrac{7,3}{36,5}=0,2\left(mol\right)\)
\(n_{CO_2}=\dfrac{1}{2}n_{HCl}=0,1\left(mol\right)\\ V_{CO_2}=0,1.22,4=2,24\left(l\right)\) 
\(m_{H_2SO_4}=\dfrac{100.9,8}{100}=9,8\left(g\right)\\ n_{H_2SO_4}=\dfrac{9,8}{98}=0,1\left(mol\right)\\ n_{Al}=\dfrac{2}{3}n_{H_2SO_4}=\dfrac{1}{15}\left(mol\right)\\ m_{Al}=\dfrac{1}{15}.27=1,8\left(g\right)\\ n_{H_2}=n_{H_2SO_4}=0,1\left(mol\right)\\ V_{H_2}=0,1.22,4=2,24\left(l\right)\) 
\(pthh:2HCl+CaCO_3\rightarrow H_2O+CaCl_2+CO_2\) 
          0,2        0,1             0,1         0,1          0,1 
\(m_{dd}=100+\left(100.0,1\right)-\left(0,1.18\right)-\left(0,1.44\right)=103,8\left(g\right)\\ C\%_{CaCl_2}=\dfrac{0,1.111}{103,8}.100\%=10,7\%\)