Chọn D.
Phương pháp: Tính đạo hàm cấp 1 và đạo hàm cấp 2.
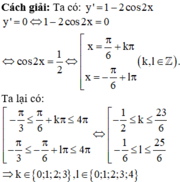
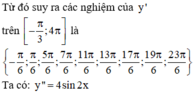
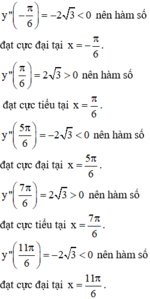
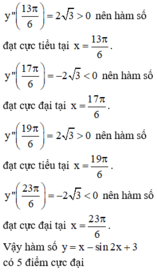
Chọn D.
Phương pháp: Tính đạo hàm cấp 1 và đạo hàm cấp 2.
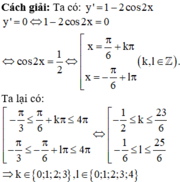
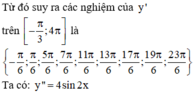
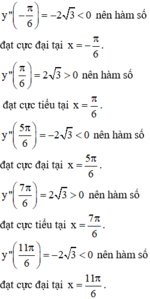
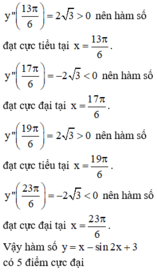
Cho hàm số y = sin2 x+2 sinx, với x∈ [ - π ; π ] . Hàm số này có mấy điểm cực trị
A. Bốn.
B. Một.
C. Ba.
D. Hai.
Trên đoạn - π ; π , hàm số y = sin x có mấy điểm cực trị ?
A. 2
B. 3
C. 4
D. 5
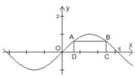
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
A. 2 2
B. 1 2
C. 1
D. 3 2
Cho hàm số y=f(x) có đạo hàm trên đoạn [a;b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn [a;b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3
Cho hàm số y=f(x)có đạo hàm trên đoạn [a,b]. Ta xét các khẳng định sau:
1) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị lớn nhất của f(x) trên đoạn[a,b]
2) Nếu hàm số f(x) đạt cực đại tại điểm x 0 ∈ a ; b thì f x o là giá trị nhỏ nhất của f(x) trên đoạn [a,b]
3) Nếu hàm số f(x) đạt cực đại tại điểm x 0 và đạt cực tiểu tại điểm x 1 x 0 , x 1 ∈ a ; b thì ta luôn có f x 0 > f x 1
Số khẳng định đúng là?
A. 1
B. 2
C. 0
D. 3
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;π/4] thỏa mãn f π 4 = 3 , ∫ 0 π 4 f x cos x d x = 1 và ∫ 0 π 4 sin x . tan x . f x d x = 2 Tích phân ∫ 0 π 4 sin x f ' x d x bằng
A. 4.
B. 2 + 3 2 2
C. 1 + 3 2 2
D. 6.
Giá trị cực đại của hàm số y = x + sin2x trên 0 ; π là:
A. π 6 + 3 2
B. 2 π 3 + 3 2
C. 2 π 3 - 3 2
D. π 3 + 3 2
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = 2 c o s 3 x - c o s 2 x trên đoạn D=[ - π / 3 ; π / 3 ]
A. m a x ( x ∈ D ) f ( x ) = 1 ; m i n ( x ∈ D ) f ( x ) = 19 / 27
B. m a x ( x ∈ D ) f ( x ) = 3 / 4 ; m i n ( x ∈ D ) f ( x ) = - 3
C. m a x ( x ∈ D ) f ( x ) = 1 ; m i n ( x ∈ D ) f ( x ) = - 3
D. m a x ( x ∈ D ) f ( x ) = 3 / 4 ; m i n ( x ∈ D ) f ( x ) = 19 / 27