Các câu hỏi tương tự
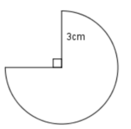
Cắt mặt xung quanh của một hình nón tròn xoay dọc theo một đường sinh rồi trải ra trên mặt phẳng ta được một nửa hình tròn bán kính R. Hỏi hình nón đó có bán kính r của đường tròn đáy và góc ở đỉnh của hình nón bằng bao nhiêu ?
Một hình nón có góc ở đỉnh bằng 90°. Hình trụ có chung trục với hình nón. Một đáy của nó thuộc mặt đáy hình nón, đáy còn lại thuộc mặt xung quanh hình nón có bán kính bằng
2
3
bán kính đường tròn đáy hình nón. Tính
k
V
T
V
N
(VT, VN là thể tích hình trụ, hình nón).
Đọc tiếp
Một hình nón có góc ở đỉnh bằng 90°. Hình trụ có chung trục với hình nón. Một đáy của nó thuộc mặt đáy hình nón, đáy còn lại thuộc mặt xung quanh hình nón có bán kính bằng 2 3 bán kính đường tròn đáy hình nón. Tính k = V T V N (VT, VN là thể tích hình trụ, hình nón).
![]()
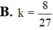
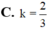
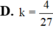
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao h1,5m gồm: - Phần dưới có dạng hình trụ bán kính đáy R1m và có chiều cao bằng
1
3
h
; - Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng
1
2
R
ở phía trên (người ta thường gọi hình đó là hình nón cụt); - Phần ở giữa rỗng có dạng hình trụ bán kính đáy bằng...
Đọc tiếp
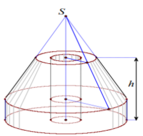
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao h=1,5m gồm:
- Phần dưới có dạng hình trụ bán kính đáy R=1m và có chiều cao bằng 1 3 h ;
- Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng 1 2 R ở phía trên (người ta thường gọi hình đó là hình nón cụt);
- Phần ở giữa rỗng có dạng hình trụ bán kính đáy bằng 1 4 R (tham khảo hình vẽ bên dưới).
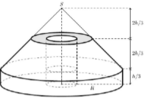
Thể tích của khối bê tông (làm tròn đến chữ số thập phân thứ ba) bằng
![]()
![]()
![]()
![]()
Cho hai mặt phẳng (P) và (Q) song song với nhau cắt khối cầu tâm O bán kính R tạo thành hai hình tròn (C1) và (C2) cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn, đáy trùng với hình tròn còn lại. Biết diện tích xung quanh của hình nón là lớn nhất, khi đó thể tích khối trụ có hai đáy là hai hình tròn (C1) và (C2) bằng: A.
4
π
R...
Đọc tiếp
Cho hai mặt phẳng (P) và (Q) song song với nhau cắt khối cầu tâm O bán kính R tạo thành hai hình tròn (C1) và (C2) cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn, đáy trùng với hình tròn còn lại. Biết diện tích xung quanh của hình nón là lớn nhất, khi đó thể tích khối trụ có hai đáy là hai hình tròn (C1) và (C2) bằng:
A. 4 π R 3 3 9
B. 2 π R 3 3 9
C. π R 3 3 9
D. 4 π R 3 3 3
Một hình nón có chiều cao SO50cm và có bán kính đáy bằng 10cm. Lấy điểm M thuộc đoạn SO sao cho OM20cm. Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn (C). Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi (C) (xem hình vẽ).
Đọc tiếp
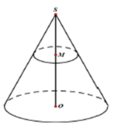
Một hình nón có chiều cao SO=50cm và có bán kính đáy bằng 10cm. Lấy điểm M thuộc đoạn SO sao cho OM=20cm. Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn (C). Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi (C) (xem hình vẽ).
![]()
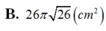

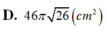
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao
h
1
,
5
m
gồm: - Phần dưới có dạng hình trụ bán kính đáy
R
1
m
và có chiều cao bằng
1
3
h
- Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng
1
2...
Đọc tiếp
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao h = 1 , 5 m gồm:
- Phần dưới có dạng hình trụ bán kính đáy R = 1 m và có chiều cao bằng 1 3 h
- Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng 1 2 R ở phía trên (người ta thường gọi là hình nón cụt);
- Phần ở giữa rỗng có dạng hình trụ, bán kính đáy bằng 1 4 R (tham khảo hình vẽ bên dưới).
Thể tích của khối bê tông (làm tròn đến chữ số thập phân thứ ba) bằng
![]()
![]()
![]()
![]()
Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là a và 2a sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Tính bán kính đáy r của hình nón đã cho. A.
r
8
a
3
B.
r
2
2
a
C.
r
4...
Đọc tiếp
Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là a và 2a sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Tính bán kính đáy r của hình nón đã cho.
A. r = 8 a 3
B. r = 2 2 a
C. r = 4 a 3
D. r = 2 a
Cho hình nón tròn xoay đỉnh S, đáy là một hìnht tròn tâm O bán kính R, chiều cao của hình nón bằng 2R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho IO 2R. Giả sử A là điểm trên đường tròn (O) sao cho OA
⊥
OI. Diện tích xung quanh của hình nón bằng:
Đọc tiếp
Cho hình nón tròn xoay đỉnh S, đáy là một hìnht tròn tâm O bán kính R, chiều cao của hình nón bằng 2R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho IO = 2R. Giả sử A là điểm trên đường tròn (O) sao cho OA ⊥ OI. Diện tích xung quanh của hình nón bằng:
![]()
![]()
![]()
![]()
Một hình trụ có bán kính đáy bằng r và khoảng cách giữa hai đáy bằng
r
3
Một hình nón có đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung quanh của hình trụ và hình nón. A.
3
B.
1
3
C.
1
3
D.
3
Đọc tiếp
Một hình trụ có bán kính đáy bằng r và khoảng cách giữa hai đáy bằng r 3 Một hình nón có đỉnh là tâm mặt đáy này và đáy trùng với mặt đáy kia của hình trụ. Tính tỉ số diện tích xung quanh của hình trụ và hình nón.
A. 3
B. 1 3
C. 1 3
D. 3