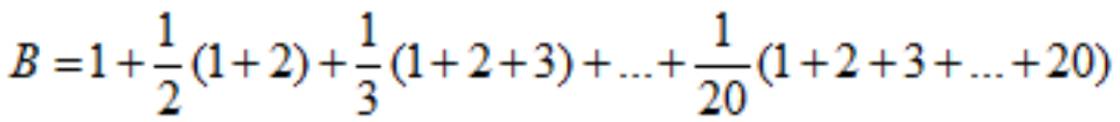Ta có: \(\dfrac{1+2+...+n}{n}=\dfrac{\dfrac{n\left(n+1\right)}{2}}{n}=\dfrac{n+1}{2}\)
Áp dụng:
\(B=1+\dfrac{1+2}{2}+\dfrac{1+2+3}{3}+...+\dfrac{1+2+...+20}{20}\)
\(=1+\dfrac{2+1}{2}+\dfrac{3+1}{2}+...+\dfrac{20+1}{2}\)
\(=1+\dfrac{3}{2}+\dfrac{4}{2}+...+\dfrac{21}{2}\)
\(=\dfrac{2+3+4+...+21}{2}\)
\(=\dfrac{1+2+3+...+21-1}{2}\)
\(=\dfrac{\dfrac{21.22}{2}-1}{2}=115\)