Đáp án A
Theo định lý Pytago ta có:
B C 2 = A B 2 + A C 2 ⇔ B C 2 = 100 ⇔ BC = 10
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
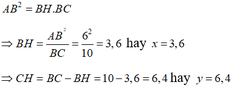
Vậy x = 3,6; y = 6,4
Đáp án A
Theo định lý Pytago ta có:
B C 2 = A B 2 + A C 2 ⇔ B C 2 = 100 ⇔ BC = 10
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
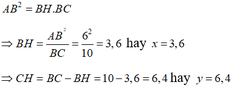
Vậy x = 3,6; y = 6,4
Cho hình vẽ. Độ dài cạnh DA là: a)6,4 B)3,6 C)7,2 D)5,4
giúp em với ạ
1. Cho đường thẳng d y=ax+2. tìm hệ số góc của của (d) biết đường thẳng đi qua điểm m (3,6)
2. Cho hàm số y=-x+3. a)vẽ đồ thị (d) của hàm số. b) tính góc a tạo bới đường thẳng y=-x+3 với trục ox
Bài 1 A) giải hệ phương trình X - 2 y = 7 2 x + y = 1 B) giải phương trình : x² - 6 + 5 = 0 Bài 2 Cho (p) = y = 2x² , (D) y = -x +3 A) vẽ (p) B) tìm tọa độ giao điểm của (p) và (D) bằng phép tính
hãy nêu tính đồng biến, nghịch biến của các hàm số bậc nhất sau:
a, y=2x-7
b, y=\(\left(1-\sqrt{2}\right)x+\sqrt{3}\)
c, y=-5x+2
d, y=\(\left(1+m^2\right)x-6\)
e, y=\(y=\left(\sqrt{3}-1\right)x+2\)
f=(2+m^2)x+1
Câu 1. Cho tam giác ABC vuông tại A có độ dài các cạnh góc vuông AB = 6 cm và AC =8 cm.Độ dài hình chiếu của các cạnh góc vuông lên cạnh huyền BH, CH là: A. 3 cm và 3,6 cm ; C. 3,6 cm và 6,4 cm B. 3,6 cm và 4,8 cm ; D. 4,8 cm và 6,4 cm Câu 2.Cho tam giác ABC vuông tại A có một góc B bằng 300 và cạnh huyền bằng 14cm. Độ dài đường cao xuất phát từ đỉnh góc vuông AH là: A. 3,5 cm ; B.7√3 /2 cm ; C. 7 cm ; D. 7√3 cm Câu 3. Tam giác ABC vuông tại A có AB = 3cm , AC = 4 cm SinB bằng: A. 0,6 ; B. 0,75 ; C. 0,8 ; D. 1,25 Câu 4. Một chiếc máy bay bay lên với vận tốc trung bình 300km/h. Đường bay lên tạo với phương nằm ngang một góc 250. Hỏi sau 3 phút máy bay bay lên đạt được độ cao là bao nhiêu mét (làm tròn đến hàng đơn vị). a,/5339 m b./6339m c./ 6km d./6.34km Câu 5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB =5cm; BC = 13cm. Độ dài CH bằng: A. 25 /3 cm B. 12/13 cm C. 5/13 cm D. 144/13cm Câu 6. Trong hình bên, tam giác ABC có góc C = 30° và AC =√6 cm. độ dài BC bằng: A. 3√6 cm B. 2√3 cm C. 3√2 cm D. 2√2 cm Câu 7. DABC vuông tại A có AB = 3cm và góc B = 60°. Độ dài cạnh AC là: A. 6cm B. 6√3 cm C. 3√3 cm D. Một kết quả khác Câu 8. Giá trị của biểu thức √4-2√3bằng A. 2 -√3 B 1 -√3 C. √3 - 1 D. √3 -2 Câu 9: Biểu thức √(1- √3)² + √ (1 +√3 ) ² bằng: A. 2√3 B. 3√3 C. 2 D. -2 Câu 10. Khi làm thực hành ngoài trời môn Toán về việc ứng dụng các tỉ số lượng giác của góc nhọn vào thực tế. Cô giáo phân công cho đội của Nam đo chiều cao của cây cổ thụ sau sân trường. Do cây quá cao không thể leo lên đo, nên cả đội tìm cách để tính chiều cao của cây. Trước tiên, bạn Nam đứng cách cây 20m mới nhìn thấy được đỉnh cây. Sau đó, tại vị trí đã chọn bạn dùng dụng cụ đo góc, nhìn lên đỉnh cây thì hướng nhìn tạo với phương nằm ngang tầm mắt (song song với mặt đất) một góc 350. Biết rằng khoảng cách từ mặt đất đến mắt của Nam là 1,6m. Tính chiều cao của cây cổ thụ (làm tròn đến mét). A. 13m B. 14m C. 15m D 16 m Câu 11. Một nhóm gồm 9 bạn sinh viên tổ chức đi du lịch hè (chi phí chuyến đi chia đều cho mỗi người). Sau khi đã hợp đồng xong, giờ chót có 2 bạn bận việc đột xuất không đi được. Vì vậy, mỗi bạn còn lại phải trả thêm 280 000 đồng so với dự kiến ban đầu. Hỏi tổng chi phí chuyến đi là bao nhiêu tiền? A. 13 860 000 đồng B. 8 820 000 đồng C. 5 040 000 đồng D. 17 640 000 đồng Câu 12. Theo quy định của cửa hàng xe máy, để hoàn thành chỉ tiêu trong một tháng, mỗi nhân viên phải bán được trung bình một chiếc xe máy trong một ngày. Nhân viên nào hoàn thành chỉ tiêu trong một tháng thì nhận lương cơ bản là 8 000 000 đồng. Nếu trong một tháng nhân viên nào vượt chỉ tiêu thì được thưởng thêm 8% tiền lời của số xe bán vượt chỉ tiêu. Trong tháng 5 (có 31 ngày), anh Thành nhận được số tiền là 9 800 000 đồng (bao gồm cả lương cơ bản và tiền thưởng thêm tháng đó). Hỏi anh Thành đã bán được bao nhiêu chiếc xe máy trong tháng 5, biết rằng mỗi xe máy bán ra thì cửa hàng thu được tiền lời là 2 500 000 đồng. A. 38 chiếc B. 40 chiếc C. 42 chiếc D. 44 chiếc Câu 13. Trong một buổi triển lãm nghệ thuật, ban tổ chức dự định trao cho tất cả số khách mời mỗi người hai phần quà. Nhưng vì có 12 khách không đến nên ban tổ chức đã tặng cho mỗi khách tham dự ba phần quà. Hỏi có bao nhiêu khách được mời tham dự buổi triển lãm? A. 20 khách B. 24 khách C. 30 khách D. 36 khách Câu 14 : Giá trị của x để √2x - 1 =-3 là: A. x =5 B. x =-1 C. x = -2 ; x= -1 D. x không có giá trị. Câu 15 : Kết quả của phép tính √12 -1/3√27 - √3 là : A. 0 B. 4√3 C. 2√3 D. -2√3
Parabol \(y=ax^2+bx+2\) đi qua điểm M ( 2 ; 3 ) và N ( -1 ; 4 ) có phương trình là :
A . \(y=x^2+x+2\)
B . \(y=\dfrac{5}{6}x^2-\dfrac{7}{6}x+2\)
C . \(y=2x^2-\dfrac{7}{2}x+2\)
D . \(y=x^2-x+2\)
Rút gọn biểu thức sau
a/ A=\(\frac{x\sqrt{y}-y\sqrt{x}}{\sqrt{xy}}+\frac{x-y}{\sqrt{x}-\sqrt{y}}\)Với x>0 ; y>0 ;x#y
b/ B=\(\frac{3}{2+\sqrt{3}}+\frac{13}{4-\sqrt{3}}+\frac{6}{\sqrt{3}}\)
c/ C=\(\frac{\sqrt{4-2\sqrt{3}}}{\sqrt{6}-\sqrt{2}}\)
d/ D=\(\left(3\sqrt{2}+\sqrt{6}\right)\sqrt{6-3\sqrt{3}}\)
Phương pháp 5. Biến đổi về dạng tổng các bình phương \(A^2+B^2+C^2=0\)
a \(x+y+12=4\sqrt{x}+6\sqrt{y-1}\)
b \(x+y+z+35=2\left(2\sqrt{x+1}+3\sqrt{y+2}+4\sqrt{z+3}\right)\)
c \(9x+17=6\sqrt{8x+1}+4\sqrt{x+3}\)
d \(\sqrt{x}+2\sqrt{x+3}=x+4\)
e\(\sqrt{3-x}+2\sqrt{3x-2}-3=x\)
b1 : rút gọn biểu thức
a: x-y/y^2 nhân căn y^4/x^2 - 2xy + y^2 với x khác y
b: căn x- 2 căn x +1/x+ 2 căn x +1 với x > 0
b2: rút gọn rồi tính giá trị
a: B= căn (x+2) ^4 / (3-x)^2 + x^2+1/x+3 với x<3 và tính b khi x= 0.5
b: C = 5x - căn 8 + căn x^3 + 2x^2/ căn x+2 cới x > -2 và tính C khi x + - căn 2
c: D= căn 3(x+y)^2/4 nhân 2/x^2-y^2 với x khác y
Rút gọn các biểu thức sau:
a) A=\(\dfrac{x\sqrt{y}+y\sqrt{x}}{x+2\sqrt{xy}+y}\)(x≥0 , y≥0 , xy≠0)
b) B=\(\dfrac{x\sqrt{y}-y\sqrt{x}}{x-2\sqrt{xy}+y}\)(x≥0 , y≥0 , x≠y)
c) C=\(\dfrac{3\sqrt{a}-2a-1}{4a-4\sqrt{a}+1}\)(a≥0 , a≠\(\dfrac{1}{4}\))
d) D=\(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\)(a≥0 , a≠4)