Các câu hỏi tương tự
Tính thể tích V của vật thể nằm giữa hai mặt phẳng x –1, x 1. Biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x
-
1
≤
x
≤
1
là một hình vuông cạnh
2
1
-
x
2
. A. ...
Đọc tiếp
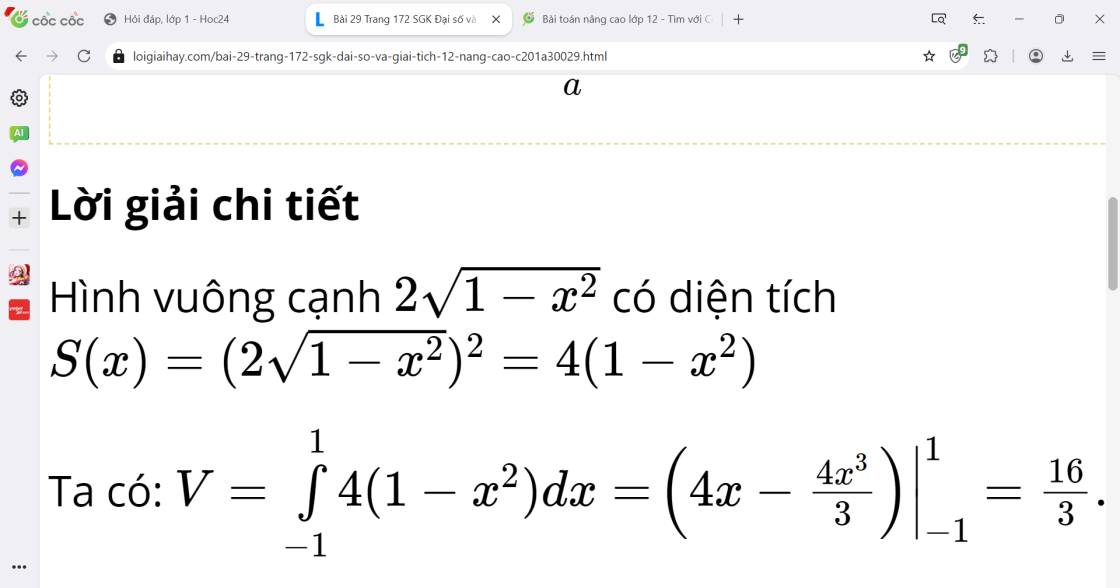
Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = –1, x = 1. Biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x - 1 ≤ x ≤ 1 là một hình vuông cạnh 2 1 - x 2 .
A. V = 13 2
B. V = 16 3
C. V = 15 4
D. V = 14 3
Một vật thể nằm giữa hai mặt phẳng x -1; x 1 và thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x là một hình tròn có diện tích bằng 3π. Thể tích của vật thể là A.
3
π
2
B.
6
π
C. 6. D.
2
π
Đọc tiếp
Một vật thể nằm giữa hai mặt phẳng x = -1; x = 1 và thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x là một hình tròn có diện tích bằng 3π. Thể tích của vật thể là
A. 3 π 2
B. 6 π
C. 6.
D. 2 π
Tính thể tích của vật thể nằm giữa hai mặt phẳng x 0 và x
3
, biết thiết diện của vật thể cắt bởi mặt phẳng (P) vuông góc với trục tại điểm có hoành độ x (
0
≤
x
≤
3
) là một hình chữ nhật có độ dài hai cạnh là x và
1
+
x
2
A. 1 B. 2 C. 7/3 D. 3
Đọc tiếp
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = 3 , biết thiết diện của vật thể cắt bởi mặt phẳng (P) vuông góc với trục tại điểm có hoành độ x ( 0 ≤ x ≤ 3 ) là một hình chữ nhật có độ dài hai cạnh là x và 1 + x 2
A. 1
B. 2
C. 7/3
D. 3
Cho (T) là vật thể nằm giữa hai mặt phẳng x 0, x 1. Tính thể tích V của (T) biết rằng khi cắt (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x,
0
≤
x
≤
1
,ta được thiết diện là tam giác đều có các cạnh bằng
1
+
x
A.
V
3
2
B.
V...
Đọc tiếp
Cho (T) là vật thể nằm giữa hai mặt phẳng x = 0, x = 1. Tính thể tích V của (T) biết rằng khi cắt (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x, 0 ≤ x ≤ 1 ,ta được thiết diện là tam giác đều có các cạnh bằng 1 + x
A. V = 3 2
B. V = 3 3 2 π
C. V = 3 3 2
D. V = 3 2 π
Tính thể tích của vật thể nằm giữa hai mặt phẳng x 0 và x 1, biết thiết diện của vật thể cắt mặt phẳng (P) vuông góc với trục Ox tại điểm có hoành độ
x
(
0
≤
x
≤
1
)
là một hình chữ nhật có độ dài lần lượt là x và
ln
(
x
2
+
1
)
A.
V
ln
2
−
1...
Đọc tiếp
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = 1, biết thiết diện của vật thể cắt mặt phẳng (P) vuông góc với trục Ox tại điểm có hoành độ x ( 0 ≤ x ≤ 1 ) là một hình chữ nhật có độ dài lần lượt là x và ln ( x 2 + 1 )
A. V = ln 2 − 1 2 .
B. V = ln 2 - 1 2 .
C. V = 1 2 l n 2 − 1.
D. V = l n 2 − 1.
Tính thể tích của vật thể nằm giữa hai mặt phẳng x 0, x 2, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x
0
≤
x
≤
2
là một nủa hình tròn đường kính
5
x
2
. A.
4
π
B.
π
C.
3...
Đọc tiếp
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0, x = 2, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 2 là một nủa hình tròn đường kính 5 x 2 .
A. 4 π
B. π
C. 3 π
D. 2 π
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x1 và x4, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (
1
≤
x
≤
4
) thì được thiết diện là một hình lục giác đều có độ dài cạnh là 2x.
Đọc tiếp
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x=1 và x=4, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x ( 1 ≤ x ≤ 4 ) thì được thiết diện là một hình lục giác đều có độ dài cạnh là 2x.
![]()
![]()
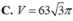
![]()
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x 1 và x 3, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và
3
x
2
-
2
Đọc tiếp
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và 3 x 2 - 2
![]()
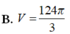

![]()
Thể tích V của vật thể nằm giữa hai mặt phẳng x 0 và x π, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ π) là một tam giác đều cạnh
2
sin
x
A. V 3 B. V 3π C.
2
3
D.
2
π
3
Đọc tiếp
Thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = π, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ π) là một tam giác đều cạnh 2 sin x
A. V = 3
B. V = 3π
C. 2 3
D. 2 π 3