Các câu hỏi tương tự
Cho khối lăng trụ đứng ABC.A’B’C’ có BBa, đáy ABC là tam giác vuông cân tại B và ACa
2
.
Tính thể tích V của khối lăng trụ đã cho
Đọc tiếp
Cho khối lăng trụ đứng ABC.A’B’C’ có BB'=a, đáy ABC là tam giác vuông cân tại B và AC=a 2 . Tính thể tích V của khối lăng trụ đã cho
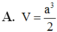
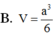
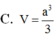
![]()
Cho khối lăng trụ đứng ABC.A’B’C’ có BBa đáy ABC là tam giác vuông cân tại B và ACa
2
. Tính thể tích V của khối lăng trụ đã cho A.
V
a
3
2
B.
a
3
6
C.
V
a...
Đọc tiếp
Cho khối lăng trụ đứng ABC.A’B’C’ có BB'=a đáy ABC là tam giác vuông cân tại B và AC=a 2 . Tính thể tích V của khối lăng trụ đã cho
A. V = a 3 2
B. a 3 6
C. V = a 3 3
D. V = a 3
Cho hình lăng trụ ngũ giác ABCD.A'B'C'D'. Gọi A'', B'', C'', D'', E'' lần lượt là trung điểm của các cạnh AA', BB', CC', DD', EE'. Tỉ số thể tích giữa khối lăng trụ ABCDE.A''B''C''D''E'' và khối lăng trụ ABCDE.A'B'C'D' bằng:
A. 1/2 B. 1/4
C. 1/8 D. 1/10.
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:A. 2
π
a
3
B. 2
π
a
3
/3C. 4
π
a
3
D.
π
a
3
Đọc tiếp
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:
A. 2 π a 3 B. 2 π a 3 /3
C. 4 π a 3 D. π a 3
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB 1, AC 2, cạnh
A
A
2
. Hình chiếu vuông góc của A’ trên mặt đáy (ABC) trùng với chân đường cao hạ từ B của tam giác ABC. Thể tích V của khối lăng trụ đã cho là
Đọc tiếp
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = 1, AC = 2, cạnh A A ' = 2 . Hình chiếu vuông góc của A’ trên mặt đáy (ABC) trùng với chân đường cao hạ từ B của tam giác ABC. Thể tích V của khối lăng trụ đã cho là
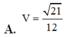
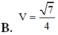
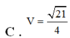
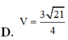
Cho một hình trụ có chiều cao bằng 2 và bán kính đáy bằng 3. Thể tích khối trụ đã cho bằng:
A . 6 π
B . 15 π
C. 9 π
D . 18 π
Cho hình lăng trụ đứng ABC.A’B’C’ có
A
B
1
,
A
C
2
,
B
A
C
^
120
0
. Giả sử D là trung điểm của cạnh CC’ và
B
D...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có A B = 1 , A C = 2 , B A C ^ = 120 0 . Giả sử D là trung điểm của cạnh CC’ và B D A ' ^ = 90 0 . Tính thể tích V của khối lăng trụ ABC.A’B’C’
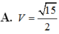
![]()
![]()
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)
Cho khối lăng trụ đứng
A
B
C
.
A
,
B
,
C
,
có
B
B
,
a
, đáy ABC là tam giác vuông cân tại B và
A
C
a
2
. Tính thể tích V của khối lăng trụ đã cho. A.
V
a
3...
Đọc tiếp
Cho khối lăng trụ đứng A B C . A , B , C , có B B , = a , đáy ABC là tam giác vuông cân tại B và A C = a 2 . Tính thể tích V của khối lăng trụ đã cho.
A. V = a 3 .
B. V = a 3 3 .
C. V = a 3 6 .
D. V = a 3 2 .
Một khối trụ có bán kính đáy bằng 2, chiều cao bằng 3. Tính thể tích V của khối trụ
![]()
![]()
![]()
![]()






