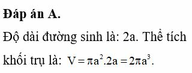Các câu hỏi tương tự
Tính thể tích của khối trụ biết bán kính đáy của hình trụ đó bằng a và thiết diện đi qua trục là một hình vuông
A. 2 πa 3
B. 2 3 πa 3
C. 4 πa 3
D. πa 3
Cho hình trụ có diện tích xung quanh bằng 4 π , thiết diện qua trục là hình vuông. Tính thể tích V của khối trụ giới hạn bởi hình trụ
A. V = 2 π
B. V = 6 π
C. V = 3 π
D. V = 5 π
Cho hình trụ có diện tích toàn phần là 4
π
và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Thể tích khối trụ đã cho bằng A.
4
π
6
9
B.
π
6
12
C.
π
6...
Đọc tiếp
Cho hình trụ có diện tích toàn phần là 4 π và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Thể tích khối trụ đã cho bằng
A. 4 π 6 9
B. π 6 12
C. π 6 9
D. 4 π 9
Một hình trụ có bán kính đáy là 2 cm. Một mặt phẳng đi qua trục của hình trụ, cắt hình trụ theo thiết diện là một hình vuông. Tính thể tích khối trụ đó. A.
4
π
(
c
m
3
)
B.
8
π
(
c
m
3
)
C.
16
π
(
c
m
3...
Đọc tiếp
Một hình trụ có bán kính đáy là 2 cm. Một mặt phẳng đi qua trục của hình trụ, cắt hình trụ theo thiết diện là một hình vuông. Tính thể tích khối trụ đó.
A. 4 π ( c m 3 )
B. 8 π ( c m 3 )
C. 16 π ( c m 3 )
D. 32 π ( c m 3 )
Cho hình trụ có bán kính đáy bằng a. Cắt hình trụ bởi một mặt phẳng song song với trục của hình trụ và cách trục của hình trụ một khoảng bằng
a
2
ta được thiết diện là một hình vuông. Tính thể tích khối trụ A.
π
a
3
3
4
B.
π
a
3
3
C. ...
Đọc tiếp
Cho hình trụ có bán kính đáy bằng a. Cắt hình trụ bởi một mặt phẳng song song với trục của hình trụ và cách trục của hình trụ một khoảng bằng a 2 ta được thiết diện là một hình vuông. Tính thể tích khối trụ
A. π a 3 3 4
B. π a 3 3
C. π a 3
D. 3 π a 3
Một khối trụ có thể tích bằng 25
π
. Nếu chiều cao khối trụ tăng lên năm lần và giữ nguyên bán kính đáy thì khối trụ mới có diện tích xung quanh bằng 25. Bán kính đáy của khối trụ ban đầu là: A.
r
10
B.
r
5
C.
r
2
D.
r
15
Đọc tiếp
Một khối trụ có thể tích bằng 25 π . Nếu chiều cao khối trụ tăng lên năm lần và giữ nguyên bán kính đáy thì khối trụ mới có diện tích xung quanh bằng 25. Bán kính đáy của khối trụ ban đầu là:
A. r = 10
B. r = 5
C. r = 2
D. r = 15
Cho hình trụ có bán kính đáy bằng 2a. Một mặt phẳng đi qua trục của hình trụ và cắt hình trụ theo thiết diện là hình vuông. Tính thể tích khối trụ đã cho A.
18
π
a
3
B.
4
π
a
3
C.
8
π
a
3
D.
16
π...
Đọc tiếp
Cho hình trụ có bán kính đáy bằng 2a. Một mặt phẳng đi qua trục của hình trụ và cắt hình trụ theo thiết diện là hình vuông. Tính thể tích khối trụ đã cho
A. 18 π a 3
B. 4 π a 3
C. 8 π a 3
D. 16 π a 3
Cho hình trụ có bán kính đáy là Ra, mặt phẳng qua trục cắt hình trụ theo một thiết diện có diện tích bằng
8
a
2
. Diện tích xung quanh của hình trụ và thể tích khối trụ là A.
16
πa
2
;
16
πa
3
B.
8
πa
2
;
4
πa...
Đọc tiếp
Cho hình trụ có bán kính đáy là R=a, mặt phẳng qua trục cắt hình trụ theo một thiết diện có diện tích bằng 8 a 2 . Diện tích xung quanh của hình trụ và thể tích khối trụ là
A. 16 πa 2 ; 16 πa 3
B. 8 πa 2 ; 4 πa 3
C. 6 πa 2 ; 6 πa 3
D. 6 πa 2 ; 3 πa 3
Cho hình trụ có bán kính đáy là R a, mặt phẳng qua trục cắt hình trụ theo một thiết diện có diện tích bằng
8
a
2
. Diện tích xung quanh của hình trụ và thể tích khối trụ là: A.
16
π
a
2
;
16
π
a
3
B.
8
π
a...
Đọc tiếp
Cho hình trụ có bán kính đáy là R= a, mặt phẳng qua trục cắt hình trụ theo một thiết diện có diện tích bằng 8 a 2 . Diện tích xung quanh của hình trụ và thể tích khối trụ là:
A. 16 π a 2 ; 16 π a 3
B. 8 π a 2 ; 4 π a 3
C. 6 π a 2 ; 6 π a 3
D. 6 π a 2 ; 3 π a 3