Đáp án B
Diện tích mặt chéo là: a 2 2 . Từ đây ta dễ dàng suy ra độ dài một cạnh của hình lập phương sẽ là a . Do đó thể tích của hình lập phương là a 3 . Chọn phương án B.
Đáp án B
Diện tích mặt chéo là: a 2 2 . Từ đây ta dễ dàng suy ra độ dài một cạnh của hình lập phương sẽ là a . Do đó thể tích của hình lập phương là a 3 . Chọn phương án B.
Cho hình hộp ABCD.A’B’C’D’ có A (1;0;0), B (2;-1;1), D (0;1;1) và A’ (1;2;1). Gọi M, N, P, Q, E, F lần lượt là giao điểm của hai đường chéo của sáu mặt hình hộp. Tính thể tích của V khối đa diện lồi hình thành bởi sáu điểm M, N, P, Q, E, F.
A. V = 1 3
B. V = 1 2
C. V = 2 3
D. V = 1
Khi cắt khối trụ (T) bởi một mặt phẳng song song với trục và cách trục của trụ (T) một khoảng bằng a 3 là được thiết diện là hình vuông có diện tích bằng 4 a 2 Tính thể tích V của khối trụ (T)?.
![]()
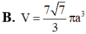

![]()
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB = a; AC =a 2 ; AD = a 3 ,(a>0) Thể tích V của khối tứ diện ABCD là:
A. V = a 3 6 3
B. V = a 3 6 6
C. V = a 3 6 2
D. V = a 3 6 9
Tính thể tích của khối lập phương có các đỉnh là trọng tâm các mặt của khối bát diện đều cạnh a
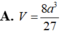
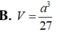
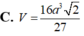
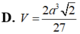
Cho tứ diện ABCD có AD ⊥ (ABC), ABC là tam giác vuông tại B. Biết
BC=A, AB=a 3 , AD=3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
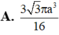
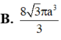
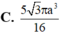
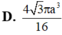
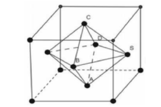
Người ta gọt một khối lập phương gỗ đê lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là các tâm của các mặt; khối lập phương). Biết các cạnh của khối lập phương bằng a. Hãy tính thể tích của khối tám mặt đều đó:
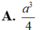
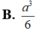
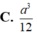
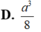
Một khối lập phương có diện tích một mặt bằng 4. Nếu tăng cạnh của khối lập phương lên gấp đôi thì thể tích khối lập phương đó bằng:
A. 27
B. 64
C. 8
D. 1
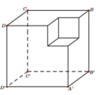
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt ![]() Tính bán kính của (S).
Tính bán kính của (S).
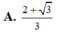
![]()

![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B. AB = BC = a 3 , góc SAB = SCB = 90 0 và khoảng cách từ A đến mặt phẳng (SBC) bằng a 2 . Thể tích khối cầu ngoại tiếp hình chóp S.ABC là
![]()
![]()
![]()
![]()