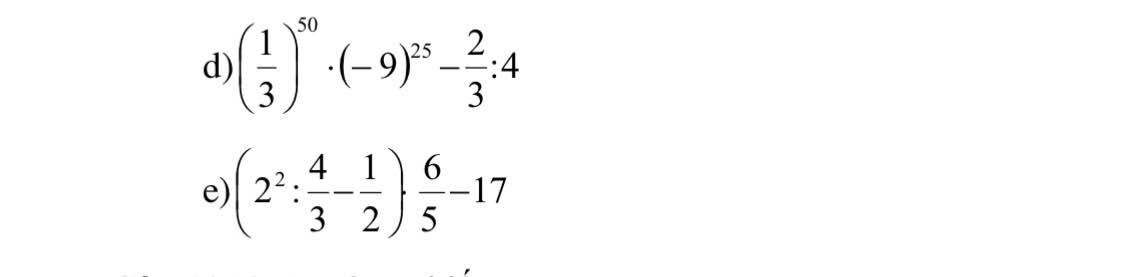\(\left(\dfrac{1}{2020}-\dfrac{2018}{2019}\right):\dfrac{2}{9}-\left(\dfrac{-2019}{2020}+\dfrac{1}{2019}\right):\dfrac{2}{3}=\)
\(\left(\dfrac{1}{2020}-\dfrac{2018}{2019}\right)\cdot\dfrac{3}{2}-\left(\dfrac{-2019}{2020}+\dfrac{1}{2019}\right)\cdot\dfrac{3}{2}=\)
\(\left[\left(\dfrac{1}{2020}-\dfrac{2018}{2019}\right)-\left(\dfrac{-2019}{2020}+\dfrac{1}{2019}\right)\right]\cdot\dfrac{3}{2}=\)
\(\left[\dfrac{1}{2020}-\dfrac{2018}{2019}-\dfrac{2019}{2020}-\dfrac{1}{2019}\right]\cdot\dfrac{3}{2}=\)
\(0\)
Đúng 0
Bình luận (0)
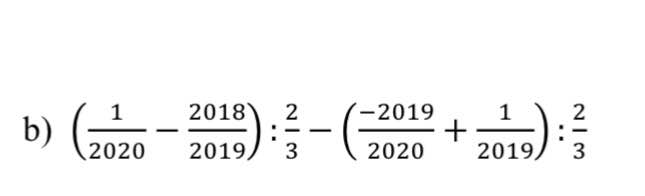
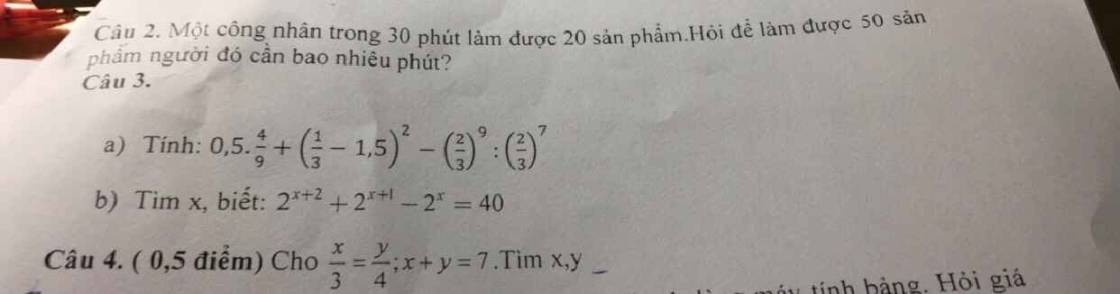Hic... làm ơn giải giúp em câu nàyT-T nhanh giúp với nếu có thể giải thích dùm cảm ơn...
