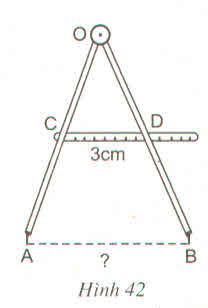
Bài giải:
Ta có CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ∆OAB.
Do đó CD = 1212AB
Suy ra AB = 2CD = 2.3 = 6cm.
Ta có: CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ΔOAB
Suy ra AB = 2CD = 2.3 = 6cm
Xét \(\Delta OAB\) có:
C là trung điểm của OA (gt)
D là trung điểm của OB (gt)
\(\Rightarrow\) CD là đường trung bình của \(\Delta OAB\) (ĐN đường TB của \(\Delta\))
\(\Rightarrow\) \(CD=\dfrac{AB}{2}\) (t/c đường TB của \(\Delta\))
\(\Rightarrow AB=2CD\)
\(\Rightarrow AB=2\cdot3\)
\(\Rightarrow AB=6\left(cm\right)\)
Vậy \(AB=6cm\)