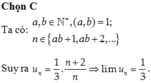Các câu hỏi tương tự
Tính giới hạn của dãy số
u
n
1
2
1
+
2
+
1
3
2
+
2
3
+
.
.
.
.
+
1
(...
Đọc tiếp
Tính giới hạn của dãy số u n = 1 2 1 + 2 + 1 3 2 + 2 3 + . . . . + 1 ( n + 1 ) n + n n + 1
A. +∞
B. -∞
C. 0
D. 1
Tính giới hạn của dãy số
u
n
1
2
1
+
2
+
1
3
2
+
2
3
+
.
.
.
+
1
(
n...
Đọc tiếp
Tính giới hạn của dãy số u n = 1 2 1 + 2 + 1 3 2 + 2 3 + . . . + 1 ( n + 1 ) n + n n + 1
A. + ∞ .
B. - ∞ .
C. 0.
D. 1.
Cho dãy số
(
u
n
)
xác định bởi
u
1
1
u
n
+
1...
Đọc tiếp
Cho dãy số ( u n ) xác định bởi u 1 = 1 u n + 1 = 2 u n + 3 u n + 2 v ớ i n ≥ 1
a) Chứng minh rằng u n > 0 với mọi n.
b) Biết ( u n ) có giới hạn hữu hạn. Tìm giới hạn đó.
Tính giới hạn của dãy số
B
l
i
m
n
6
+
n
+
1
3
-
4
n
4
+
2
n...
Đọc tiếp
Tính giới hạn của dãy số B = l i m n 6 + n + 1 3 - 4 n 4 + 2 n - 1 ( 2 n + 3 ) 2
A. +∞
B. -∞
C. 3
D. -3/4
Bài 1. (1,0 điểm) Tính giới hạn: $\lim(\sqrt{{{n}^{2}}+1}-n)$.
Tính giới hạn của dãy số
u
n
(
n
+
1
)
1
3
+
2
3
+
.
.
.
+
n...
Đọc tiếp
Tính giới hạn của dãy số u n = ( n + 1 ) 1 3 + 2 3 + . . . + n 3 3 n 3 + n + 2 :
A. + ∞ .
B. - ∞ .
C. 1 9 .
D. 1.
Tính giới hạn của dãy số
u
n
(
n
+
1
)
1
3
+
2
3
+
.
.
.
.
+...
Đọc tiếp
Tính giới hạn của dãy số u n = ( n + 1 ) 1 3 + 2 3 + . . . . + n 3 3 n 2 + n + 2
A. +∞
B. -∞
C. 1/9
D. 1
Tính giới hạn của dãy số Dlim
n
2
+
n
+
1
-
2
n
3
+
n
2
-
1...
Đọc tiếp
Tính giới hạn của dãy số D=lim n 2 + n + 1 - 2 n 3 + n 2 - 1 3 + n .:
A. + ∞ .
B. - ∞ .
C. - 1 6 .
D. 1.
Tính giới hạn của dãy số
D
l
i
m
(
n
2
+
n
+
1
-
2
n
3
+
n
2
-
1
3...
Đọc tiếp
Tính giới hạn của dãy số D = l i m ( n 2 + n + 1 - 2 n 3 + n 2 - 1 3 + n )
A. +∞
B. -∞
C. -1/6
D. 1/3