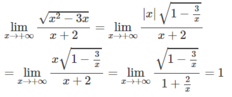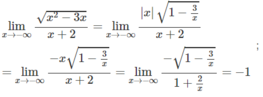Các câu hỏi tương tự
Tính giới hạn của các hàm số sau khi x → +∞ và khi x → -∞ f x = x + x 2 - x + 1
Tính giới hạn của các hàm số sau khi x → +∞ và khi x → -∞ f x = x 2 - x - x 2 + 1
Tìm a để hàm số sau có giới hạn khi
x
→
2
f
(
x
)
x
2
+
a
x
+
2
khi
x
2...
Đọc tiếp
Tìm a để hàm số sau có giới hạn khi x → 2
f ( x ) = x 2 + a x + 2 khi x > 2 2 x 2 − x + 1 khi x ≤ 2
A. + ∞
B. − ∞
C. 1 2
D.1
Gọi `bb A` là giới hạn của hàm số `f(x)=[x+x^2+x^3+...+x^50 -50]/[x-1]` khi `x -> 1.` Tính giá trị của `bb A.`
Cho hàm số
f
(
x
)
x
2
-
5
k
h
i
x
≥
3
...
Đọc tiếp
Cho hàm số f ( x ) = x 2 - 5 k h i x ≥ 3 ( 1 ) x 2 - 5 x + 2 k h i x < 3 ( 2 )
Trong biểu thức (2) ở trên, cần thay số 5 bằng số nào để hàm số f(x) có giới hạn khi x → 3?
A. 19.
B. 1.
C. -1.
D. Không có số nào thỏa mãn.
Giới hạn của hàm số
f
(
x
)
x
2
-
(
a
+
2
)
x
+
a
+
1
x
3
-
1
khi x → 1 bằng: A.
-
a
3
B. ...
Đọc tiếp
Giới hạn của hàm số f ( x ) = x 2 - ( a + 2 ) x + a + 1 x 3 - 1 khi x → 1 bằng:
A. - a 3
B. a 3
C. - a - 2 3
D. 2 - a 3
Cho hai hàm số
f
(
x
)
x
2
và có
g
x
-
x
2
+
2
...
Đọc tiếp
Cho hai hàm số f ( x ) = x 2 và có g x = - x 2 + 2 n ế u x ≤ 1 2 n ế u - 1 < x < 1 - x 2 + 2 n ế u x ≥ 1 đồ thị như hình 55
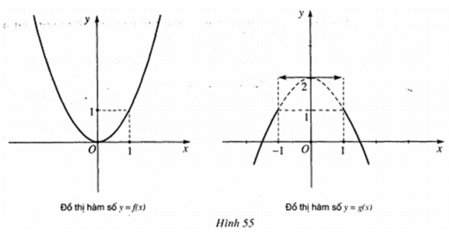
a) Tính giá trị của mỗi hàm số tại x = 1 và so sánh với giới hạn (nếu có) của hàm số đó khi x → 1 ;
b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ x = 1 .
Tìm a để hàm số
f
(
x
)
5
a
x
2
+
3
x
+
2
a
+
1
k...
Đọc tiếp
Tìm a để hàm số f ( x ) = 5 a x 2 + 3 x + 2 a + 1 k h i x ≥ 0 1 + x + x 2 + x + 2 k h i x < 0 có giới hạn tại x → 0
A. +∞
B. -∞
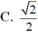
D. 1
Xét hàm số
f
x
2
x
2
-
2
x
x
-
1
1. Cho biến x những giá trị khác 1 lập thành dãy số
x
n
,
x
n...
Đọc tiếp
Xét hàm số f x = 2 x 2 - 2 x x - 1
1. Cho biến x những giá trị khác 1 lập thành dãy số x n , x n → 1 như trong bảng sau:

Khi đó, các giá trị tương ứng của hàm số
f ( x 1 ) , f ( x 2 ) , … , f ( x n ) , …
cũng lập thành một dãy số mà ta kí hiệu là f ( x n ) .
a) Chứng minh rằng f ( x n ) = 2 x n = ( 2 n + 2 ) / n .
b) Tìm giới hạn của dãy số f ( x n ) .
2. Chứng minh rằng với dãy số bất kì x n , x n ≠ 1 và x n → 1 , ta luôn có f ( x n ) → 2 .
(Với tính chất thể hiện trong câu 2, ta nói hàm số f x = 2 x 2 - 2 x x - 1 có giới hạn là 2 khi x dần tới 1).