Question

Tính diện tích hình phẳng (phần được tô đậm) như hình vẽ dưới đây

A. S = 2 3 − 2 3

B. S = 28 3

C. S = 29 3

D. S = 3 2 − 1 3

Answer 1

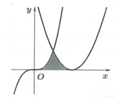
Đáp án A

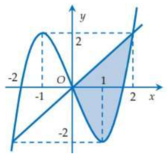
Cách 1: Xét phương trình:

x 2 = 3 ⇔ x = ± 3 ; x 2 = 1 ⇔ x = 1

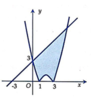
Quan sát hình vẽ:

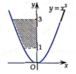
Diện tích hình phẳng giới hạn bởi các đường y = x 2 , y = 3, x = 0 là

S 1 = ∫ − 3 0 x 2 − 3 d x = ∫ − 3 0 x 2 − 3 d x = x 3 3 − 3 x 0 − 3 = 2 3  

(đvdt).

 

Diện tích hình phẳng giới hạn bởi các đường y = x 2 , y = 1, x = 0 là

S 2 = ∫ − 1 0 x 2 − 1 d x = ∫ − 1 0 x 2 − 1 d x = x 3 3 − x 0 − 1 = 2 3

 (đvdt).

 

Vậy diện tích hình phẳng cần tính là S = S 1 − S 2 = 2 3 − 2 3  (đvdt).

Cách 2: Ta có y = x 3 ⇔ y ≥ 0 x = ± y . Từ hình vẽ ta thấy x < 0 ⇒ x = − y .

Diện tích hình phẳng cần tính là:

S = ∫ 1 3 − y − 0 d y = ∫ 1 3 y d y = 2 y 3 3 3 1 = 2 3 − 2 3

 (đvdt).