Các câu hỏi tương tự
Một vật thể có mặt đáy nằm trong mặt phẳng tọa độ (Oxy) được giới hạn bởi đường cong
y
2
4
x
và đường thẳng x 4. Thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox là một nửa hình elip có trục lớn gấp đôi trục nhỏ. Tính thể tích của vật thể A.
8
π
B.
16
π
C.
32
π
D.
64
π
Đọc tiếp
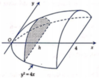
Một vật thể có mặt đáy nằm trong mặt phẳng tọa độ (Oxy) được giới hạn bởi đường cong y 2 = 4 x và đường thẳng x = 4. Thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox là một nửa hình elip có trục lớn gấp đôi trục nhỏ. Tính thể tích của vật thể
A. 8 π
B. 16 π
C. 32 π
D. 64 π
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
∆
đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng
∆
một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S. A.
36
2
π
B.
18
π
C.
36
π...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ đi qua gốc tọa độ O và điểm I(0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng ∆ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.
A. 36 2 π
B. 18 π
C. 36 π
D. 18 2 π
Trong mặt phẳng với hệ tọa độ Oxy, cho hình (H1) giới hạn bởi các đường
y
2
x
,
y
-
2
x
, x4; hình (H2) là tập hợp tất cả các điểm M(x;y) thỏa mãn các điều kiện
x
2
+
y
2
≤
16
;...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho hình (H1) giới hạn bởi các đường y = 2 x , y = - 2 x , x=4; hình (H2) là tập hợp tất cả các điểm M(x;y) thỏa mãn các điều kiện x 2 + y 2 ≤ 16 ; x - 2 2 + y 2 ≥ 4 ; x + 2 2 + y 2 ≥ 4 . Khi quay (H1);(H2) quanh Ox ta được các khối tròn xoay có thể tích lần lượt là V1, V2 .Khi đó, mệnh đề nào sau đây là đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S. A. 36π B. 36
2
π C. 18
2
π D. 18 π
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.
A. 36π
B. 36 2 π
C. 18 2 π
D. 18 π
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0; 1; 1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S. A. 36π B.
36
2
π
C.
18
2
π
D. 18π
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0; 1; 1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.
A. 36π
B.
36
2
π
C. 18 2 π
D. 18π
Trong mặt phẳng tọa độ Oxyz, gọi
(
H
1
)
là hình phẳng giới hạn bởi các đường
y
x
2
4
;
y
-
x
2
4
; x4; x -4 và
(
H
2
)...
Đọc tiếp
Trong mặt phẳng tọa độ Oxyz, gọi ( H 1 ) là hình phẳng giới hạn bởi các đường y = x 2 4 ; y = - x 2 4 ; x=4; x = -4
và ( H 2 ) là hình gồm tất cả các điểm (x;y) thỏa mãn x 2 + y 2 ≤ 16 ; x 2 + ( y - 2 ) 2 ≥ 4 ; x 2 + ( y + 2 ) 2 ≥ 4
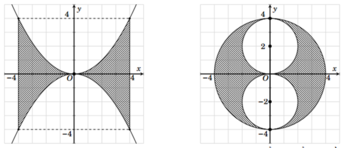
Cho H 1 và H 2 quay quanh trục Oy ta được các vật thể có thể tích lần lượt là V 1 , V 2 . Đẳng thức nào sau đây đúng?
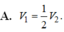
![]()
![]()
Cho hàm số
y
a
x
4
+
b
x
2
+
c
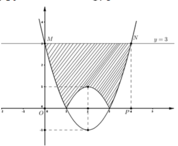
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳn...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x = 0; x=2 có diện tích bằng
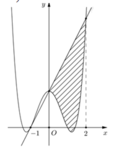
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x = 0 có diện tích bằng:
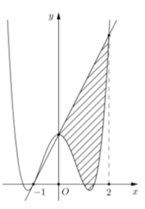
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Vẽ đồ thị của các hàm số ứng với các giá trị a, b, c và d tìm được trên cùng một mặt phẳng tọa độ. Tính diện tích của hình phẳng giới hạn bởi hai đường cong trên.